Technical Library
Our extensive technical library has just about everything you need from cable length effects to glossaries to system calibrations and load cell troubleshooting. If you don’t find what you need, just hit the “contact us” button!

Our extensive technical library has just about everything you need from cable length effects to glossaries to system calibrations and load cell troubleshooting. If you don’t find what you need, just hit the “contact us” button!

This document defines the terminology and performance parameters pertaining to engineering specifications of load cell products.
The objective of this terminology standard is to promote effective communication of specifications and to constitute a reference for uniformity.
The definitions herein are generally compatible with common understanding in the load cell community and are an expansion of those found in Load Cell Terminology and Test Procedure Recommendations, Third Edition, 1985, Scale Manufacturers Association, and in OIML International Recommendation R60, 1991 Edition.
This document includes modifications to the definitions in the above referenced standards to correct some of their inconsistencies and inadequacies.
All abbreviations are case-specific, are not to be pluralized, and do not use trailing periods.
| ampere combined error degree Celsius degree Fahrenheit degree Kelvin foot foot-pound 1 full scale gram gram force hertz inch inch-pound 2 kilogram kilogram force kiloohm kilonewton kilonewton-meter kilopound-foot kilopound-inch kilopound (kip) kilopound force megaohm |
A CE °C °F °K ft ft-lb FS g gf Hz in in-lb kg kgf Kohm kN kNm Klbf-ft Klbf-in K Klbf Mohm |
meganewton meter milliampere millimeter millivolt millivolt/volt minimum dead load newton newton-meter ohm ounce-inch pound pound-foot pound-inch pound force pound per square inch rated output static error band ton, metric volt volt direct current volt alternating current watt |
MN m mA mm mV mV/V MDL N Nm ohm oz-in lb lb-ft lb-in lbf psi RO SEB t V VDC VAC W |
|
| Note 1 – pound-foot is preferred Note 2 – pound-inch is preferred |
||||
LowProfile™ Load Cells
The Best Just Got Better!
Performance Improvement with No Price Increase
Click the images on the left to view them enlarged.
Scroll down to the bottom of this page for a PDF download.
Introducing Interface’s Enhanced
LowProfile™ Load Cell
Interface Inc. pioneered the first Low Profile™ load cell in 1969 and is the largest producer of them in the world. We guarantee that our load cells will out perform our competitors…PERIOD.
Interface Blue…
Setting the Standard in Force Measurement
Interface is Raising the Bar In High Performance Force Measurement
A 20% improvement in performance based on over 2 years of extensive engineering development
UNPARALLELED RELIABILITY
Performance Parameters That Set Us Apart From Our Competitors
World Leading Performance Begins at the Core of Our Product
Proprietary Strain Gages
Temperature Effects
Calibration
Interface Moment Compensation
Options available for a variety of applications
Interface LowProfile™Load Cells
We Recalibrate ALL Manufacturers’ Load Cells
For high accuracy force measurement the effects of the cable on the measurement must be considered. For constant voltage excitation there are two effects of significance.
These are:
If the load cell is sold with a cable of any length, the sensitivity is determined with the installed cable in calibration and this is not a problem. For load cells with connectors, or if the customer adds cable himself, there will be a loss of sensitivity of approximately 0.37% per 10 feet of 28 gage cable and 0.09% per 10 feet of 22 gage cable. This error can be eliminated if a six wire cable is run to the end of the load cell cable or connector and used in conjunction with an indicator that has sense lead capability.
Since cable resistance is a function of temperature, the cable response to temperature change affects the thermal span characteristics of the load cell/cable system. For 6-wire systems this effect is eliminated. For 4-wire cables the effect is compensated for in the standard cable lengths offered with the load cells if the load cell and cable are at the same temperature at the same time. For non-standard cable lengths, there will be an effect on thermal span performance. The effect of adding 10 feet of 28 gage cable is to cause a decrease in sensitivity with temperature equal to 0.0008%/°F (an amount equal to the standard Interface specification). For an added 10 feet of 22 gage cable the effect is to decrease sensitivity by 0.0002%/°F (one-fourth Interface spec). In many cases a customer can tolerate the degraded performance since our standard specification is extremely tight. However, for long cable runs or high accuracy applications, this can be a significant factor. In such cases, the best approach to the problem is to run six wires to the end of the standard cable length and sense the excitation voltage at that point. This eliminates the problem.
Figure 33. Simple column cell
All Interface, Inc. products are designed around either the bending beam, the shear beam, or the pipe column. In order to understand the reasons behind this decision, we need to understand the design of the plain column cell, the other major type of load cell.
The cross-section view in Figure 33 shows the components of the simple column cell. The “flexure” is the heavy column (A) running up the center of the cell, with massive blocks at the top and bottom and a thin, usually square, column in the center. This column, plus the heavy outer shell and the diaphragms (B) are the basic support elements for the measurement flexure, the column (A) which runs from S1 to S2 .
The column stress between S1 and S2 is about the same anywhere along its length, so the main gages (C1 and C2) are placed in the center, at Sg. Compensation for the nonlinearity of the column design is accomplished by the semiconductor gage (F).
Loads are applied by the customer’s fixtures which can be screwed into the threaded holes at the top and bottom ends of the column.
The “doghouse” on the side of the casing contains the bridge compensating resistors (D) which are wired (E) to the gages.
At first glance, this might seem to be an uncomplicated design. The physical parts themselves are relatively simple to produce. However, several characteristics seriously restrict its usability.
By contrast, the LowProfile cell compares dramatically better in all respects to the simple column cell.
Force and torque transducers must be calibrated in a laboratory in order to be useful in their intended application. Applications of transducers range from basic process measurements to critical calibration of other transducers or equipment. The laboratory calibration consists of loading the transducer with known masses and lever arms, or using a comparison method where load is generated by hydraulic or pneumatic means and the transducer under test is compared to a reference transducer. In either method, the cost of calibration equipment rises rapidly with increasing capacity.
Many calibration laboratories have the means to calibrate force up to about 10,000 lbf and torque up to about 20,000 lb-in, but capability for higher ranges is scarce. In fact, there are a very limited number of laboratories in the United States that have the capability for force over 200,000 lbf and torque over 100,000 lb-in.
There has been a practice in the past by some manufacturers of transducers to calibrate a high capacity transducer at partial capacity, leaving the owner to go on hoping and guessing for the sensitivity of the upper end of the capacity. This gives rise to the concept of extrapolating the partial capacity calibration to full capacity, thereby providing the possibility for an increase in confidence in the extended range.
Strain gage transducers are basically linear. That is, the output follows the input at a near constant ratio. The nonlinearity is routinely measured and typically is in range of ± 0.10%FS or less. This provides for the ability to interpolate values between calibration points with near zero error. However, the same is not true for extrapolation, which is really estimating values that are beyond the observable range. Conventional wisdom has it, and logically so, that extrapolation is not a valid method of calibration. Extrapolating is similar to forecasting, and that idea helps one realize the liability of it.
The various methods of extrapolation are not all equal. The purpose of this paper is to explore a method that has reasonable validity when economic considerations do not permit a full capacity calibration.
The use of load cells and a data logging system are a necessity in the majority of situations where materials, parts, or assemblies are fatigue tested to destruction. This is true because an accurate record of the forces at every moment of the tests is the only way that an engineer can analyze the stresses which occurred in the moments just prior to the ultimate failure. No one can accurately predict exactly when the failure will occur, nor which part of an assembly will be the weakest link which eventually fails.
When designing a test protocol, serious thought should be given to the possibility that some of the parameters of the test will need to be changed as the result of information learned in the early test cycles. It may be that the test frequencies, force levels, location or angle of force application, or phasing of test waves will need to be changed. It is therefore prudent to start out with equipment which can accommodate an increase, a decrease, or other change without a major redesign of fixtures or a major expenditure to convert or replace high cost test equipment.
“Fatigue Rated” is an exact Interface specification which defines a special class of load cell design and construction.
Not all manufacturers adhere strictly to the stringent discipline necessary to produce true fatigue rated load cells on a consistent basis. By contrast, the history of Interface Low Profile cells shows a zero return rate due to fatigue failure, for fatigue-rated cells used within ratings.
Although Interface does not recommend it, there are times when circumstances force a user to apply a large number of test cycles on a non-fatigue-rated cell. The following guidelines may assist the user in deciding how long to carry on such a test before installing the properly sized fatigue-rated cell.
If this were the only failure mode, any Interface steel or stainless steel cell could be used as a fatigue cell, if operated below 500/0 of its rated capacity. However, other minor failure modes would take over, because the load cell would be missing the “hand crafted” steps of the manufacturing process.
Many test protocols require a fixed load plus a dynamic load to be applied to a test sample simultaneously. An Interface fatigue-rated load cell is well suited to this type of application. However, there are limitations which should be applied to the loadings, to insure that the cell will be operating in its linear range and to avoid overloading the load cell or reducing its fatigue life.
The Goodman Curve shown in Figure 50 is a useful nomograph (visual calculating graph) for easily figuring combined loading limits for fatigue-rated cells. Notice that the dynamic loading limit by itself is 100% of the fatigue rating, and the static loading limit by itself is 2000/0 of the fatigue rating. In between these two end points, the limit is the diagonal straight line which connects the end points.
The Goodman Curve applies only to fatigue-rated cells. Using it to calculate combined loadings on a standard load cell could result in damage to the cell.
In the example shown on the graph the dashed line indicates a situation where we want to apply a fixed load of 70%, and we want to know how much dynamic load we can apply simultaneously. By taking a straight horizontal line at the “70% Static Load” level across to the limit line and then projecting downward from that intersection, we find that the intersection on the dynamic scale at “65% of Rated Fatigue Capacity.” This means that, on a 1000 lbf rated fatigue cell, we could apply a fixed load of 700 lbf combined with a dynamic load of 650 lbf peak in both modes.
Checking the graph, note that if we needed to apply a fixed load of 160%, we could still apply a dynamic load of 20% for a total load which varies between 140% (lower peak) and 180% (upper peak). This would mean that the cell would be operating outside the limit of the normal factory calibration on fatigue cells of 100%. If the utmost accuracy is desired, it might be advisable to have a static calibration done on the cell up to 200%, which can be done on a fatigue-rated cell by special order.
Interface has specialized in fatigue-rated load cells and their applications since its founding in 1968. Fatigue rating is a distinct specification which guarantees the customer a load cell which has a service life of 100 million fully reversed loading cycles at full rated capacity.
The very first products at Interface were fatigue-rated load cells, and over the years a history has been built up by thousands of cells in use all over the world. Many have been supplied to major manufacturers of materials test machines and to major aerospace manufacturers, for use in long term structural fatigue test programs on aircraft, space, and automotive equipment. No fatigue failure of any fatigue-rated Interface load cell, used within its ratings, has ever been reported.
It is well known that metals will fail in a statically loaded situation if the yield strength is exceeded. In as much as load cells are structural members which are stressed in the course of their normal use, they are commonly given ultimate overload ratings in an effort to characterize the magnitude of static load they will withstand without failing structurally.
However, all metal structures, including load cells, are also subject to failure as a result of repetitive loadings which are much lower than the ultimate overload rating. This phenomenon is known as a fatigue failure, and it is due to the fact that the stress which a metal can withstand under cyclic loading usually becomes less and less as the number of cyclic loadings is increased.
The cause of this apparent anomaly can be explained by noting that metals are typically not perfectly homogeneous solids. They are composed of crystals, and at locations called grain boundaries, along slip planes or in a region of a microscopic defect there can be minute strains under load which do not completely reverse during unload, leaving the material with a slight plastic deformation at the end of each complete cycle. This effect is highly dependent on the magnitude of the load and the number of cycles.
It is generally acknowledged that a structural fatigue failure develops in three stages:
Accurate prediction of fatigue life of any structure is not a reality. Well controlled tests on the most simple configurations of test specimens result in a wide scatter band of results. With complex structures typical of a load cell, analysis is even more complex. Theoretical analysis can produce approximations, however, which can be useful in estimating the margin of safety at which a particular load cell design is operating.
In materials science, the S-N curve is a well known tool. It is a graphical representation of the number of load cycles required to break a specimen, at a range of peak cyclic stress levels. S-N curves for the high quality materials used in Interface load cells have been experimentally determined, and are shown in Figure 1 for stainless steel and alloy steel, and in Figure 2 for aluminum alloy.
Thus, if the stress level is known, the fatigue life can be approximately known. However, there are factors which make fatigue life difficult to characterize.
Components Subject to Failure
There are two metal components in a load cell that must be considered in fatigue analysis, the flexure (spring element) and the strain gage (sensor).
The relative propensity to first encounter flexure or strain gage fatigue failure depends upon the design of the transducer.
Flexures
There are several metals used for flexures in Interface load cells including aircraft quality alloy steel, stainless steel, and high strength fatigue-resistant aluminum alloy. S-N curves for these three materials are presented in Figure 1 and Figure 2.
Stress is normally expressed in units of psi (pounds per square inch), but for convenience we use units of Ksi which are equal to 1000 psi. Shear stress is on the vertical axis, corresponding to the state of stress in Low Profile load cells. Readers with some materials science familiarity will recognize that classical fatigue strength for these materials is higher than indicated in the figures. This is because classical data is for bending or direct stress, whereas Interface fatigue-rated cells operate in shear mode. This analysis therefore appropriately uses the required factor for shear, avoiding a falsely optimistic result.
Note that the shear S-N curve for steel becomes essentially flat at about 55 KSI. This is a characteristic of steel. The stress level at the flat portion of the curve is called the endurance limit. If operated below this limit, theoretically the material will endure an infinite number of load cycles. Nonferrous metals do not generally exhibit an endurance limit, their curves continuing on with a small slope.
Gages
Interface strain gages are specially made of fatigue-resistant nickel-chromium alloy. Strain gage fatigue characteristics are most conveniently viewed in terms of strain rather than stress. Figure 3 shows a Strain-N curve for Interface strain gage material. Strain is a dimensionless quantity of normally very small magnitude. The microstrain unit is simply 106 strain units and is used for convenience. Stress and strain for any particular material are related by a constant which is the modulus of elasticity (30X106 for steel and 10X106 for aluminum), allowing convenient comparison of S-N curves and Strain-N curves.
The curves in Figures 1, 2, and 3 are for fully reversed load cycles, meaning that for 2000 microstrain as an example, a cycle starts at zero load and consists of one load to (+2000), one load to (-2000), with a return to zero.
Comparison of Loading Levels
Superimposed on the curves are operating levels of Interface Low Profile load cells by model series. This provides a convenient visualization of the fact that all of these load cells are designed to have very long, if not infinite, theoretical fatigue lives. Remember that in actual practice things are not necessarily so ideal. Therefore, in order to establish the correlation between theoretical and realizable fatigue life, actual test results are desirable.
Test Protocol
Interface conducted Design Verification Tests to substantiate the theoretical life predictions by means of actual load tests of the product. Obviously, building up millions of load cycles on a high capacity load cell is not a trivial task. Many hours of costly machine time are required. Tests were conducted on three representative Interface Low Profile load cells: (1) an aluminum cell of 5,500 lbf capacity, (2) a steel cell of 11,000 lbf capacity, and (3) a steel cell of 22,000 lbf capacity.
Loading to 130% of rating was selected as an acceleration factor, to bring down the test time to a realizable length, since 100 million cycles at 1 hertz and 100% loading would consume 3 years and 2 months of testing, 24 hours per day. Based on the slopes of the S-N curves, a cycle acceleration factor of at least 10 can be achieved with 130% loading, thus ensuring that the more stringent test at 107 cycles will prove a fatigue life of 108 cycles at 100% loading.
Test Results
Analysis of the test data showed that there were no indications of fatigue failure nor degradation of load cell performance outside specified limits, for the critical load cell parameters of output, zero balance, nonlinearity, hysteresis, and creep, during or after completion of the Verification Test program.
Lower Stress by Design
Interface load cells are designed for optimum fatigue life. Other load cells are not necessarily equivalent. Table 1 below is a comparison of actual strain levels in Low Profile™ and typical competitive load cells. The safety factors are a means of visualizing the design merit of the various designs. The value of fatigue rated load cells for fatigue applications is evident from the safety factor data. It is also apparent that Interface load cells with 4 mV/V output have lower stress levels and, therefore, more fatigue resistance than competitors’ cells, even though their output is only 3 mV/V or less.
Lower Stress by User Limits
Note that the tests and S-N curves are based on fully reversed load cycles. This type of loading cycle is considerably more stringent than unidirectional loading, which is the more common application of load cells. If a fatigue load cell is repeatedly loaded in only one direction, the Goodman Law predicts that it can be loaded to about 133% of the bidirectional fatigue-rated capacity with no degradation of its fatigue rating. Conversely, unidirectional loading to a fatigue cell’s rated capacity is much less stressful on the cell than bidirectional loading and can be expected to yield a fatigue life well beyond the number of cycles which could be reasonably and economically applied in a verification test program.
Excitation Voltage
Interface load cells all contain a full bridge circuit, which is shown in simplified form in Figure 1. Each leg is usually 350 ohms, except for the model series 1500 and 1923 which have 700 ohm legs.
…
Print or Download The Entire Document
Copyright 1998–2009, Interface Inc. All rights reserved.
Interface, Inc. makes no warranty, either expressed or implied, including, but not limited to, any implied warranties of merchantability or fitness for a particular purpose, regarding these materials, and makes such materials available solely on an “as-is” basis.
In no event shall Interface, Inc. be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of use of these materials.
For convenience, terms which are defined in this standard are printed in UPPER CASE when used in the definition of another term.
– The temperature of the medium surrounding the LOAD CELL.
– A load applied along the PRIMARY AXIS.
– The change in ZERO BALANCE due to a change in ambient barometric pressure. Normally expressed in units of %RO/atm.
– The comparison of LOAD CELL OUTPUT against standard test loads.
– The maximum AXIAL LOAD a LOAD CELL is designed to measure within its specifications.
– The maximum deviation of the CALIBRATION curve from the straight line drawn between MINIMUM LOAD OUTPUT and MAXIMUM LOAD OUTPUT, normally expressed in units of %FS. Both ascending and descending curves are considered.
– The change in LOAD CELL SIGNAL occurring with time while under load and with all environmental conditions and other variables remaining constant. Normally expressed in units of % of applied load over a specified time interval. It is common for characterization to be measured with a constant load at or near CAPACITY.
– The change in LOAD CELL SIGNAL occurring with time immediately after removal of a load which had been applied for a specified time interval, environmental conditions and other variables remaining constant during the loaded and unloaded intervals. Normally expressed in units of % of applied load over a specified time interval. Normally the applied interval and the recovery interval are equal. It is common for characterization to be measured with a constant load at or near CAPACITY.
– The difference between LOAD CELL SIGNAL immediately after removal of a load which had been applied for a specified time interval, environmental conditions and other variables remaining constant during the loaded interval, and the SIGNAL before application of the load. Normally expressed in units of % of applied load over a specified time interval. It is common for characterization to be measured with a constant load at or near CAPACITY.
– The displacement of the point of AXIAL LOAD application in the PRIMARY AXIS between the MDL and MDL+CAPACITY load conditions.
– Any load applied parallel to but not concentric with the PRIMARY AXIS.
– The OUTPUT corresponding to MAXIMUM LOAD in any specific test or application.
– The algebraic difference between OUTPUT at a given load descending from MAXIMUM LOAD and OUTPUT at the same load ascending from MINIMUM LOAD. Normally expressed in units of %FS. It is common for characterization to be measured at 40-60% FS.þ
– The resistance of the LOAD CELL circuit measured at the excitation terminals with no load applied and with the output terminals open-circuited.
– The DC resistance measured between the bridge circuit and the case. Normally measured at 50 VDC.
– A device which produces an OUTPUT proportional to an applied force load.
– The maximum AXIAL LOAD which can be applied without producing a permanent shift in performance characteristics beyond those specified. Normally expressed in units of % CAPACITY.
– The highest load in a specific test or application, which may be any load up to and including CAPACITY +MINIMUM LOAD, but may not exceed CAPACITY significantly.
– The maximum AXIAL LOAD which can be applied without producing a structural failure. Normally expressed in units of % CAPACITY.
– The maximum moment with respect to the PRIMARY AXIS which can be applied without producing a permanent shift in performance characteristics beyond those specified.
– The maximum torque which can be applied concentric with the primary axis without producing a permanent shift in performance characteristics beyond those specified.
– The maximum SIDE LOAD which can be applied without producing a permanent shift in performance characteristics beyond those specified.
– The difference between MAXIMUM LOAD and MINIMUM LOAD in a specific test or application. It may not exceed CAPACITY.
– The smallest load for which specified performance will be met. It is normally equal to or near NO LOAD in single mode applications and is of necessity equal to NO LOAD in double mode applications.
– The lowest load in a specific test or application, differing from NO LOAD by the weight of fixtures and load receptors which are attached plus any intentional pre-load which is applied.
– The direction of load. Tension and Compression are each one mode.
– The frequency of free oscillations under conditions of NO LOAD.
– The condition of the LOAD CELL when in its normal physical orientation, with no force input applied, and with no fixtures or load receptors attached.
– The algebraic difference between OUTPUT at a specific load and the corresponding point on the straight line drawn between MINIMUM LOAD and MAXIMUM LOAD. Normally expressed in units of %FS. It is common for characterization to be measured at 40-60 %FS.
– The maximum difference between OUTPUT readings for repeated loadings under identical loading and environmental conditions. Normally expressed in units of %RO.
– The algebraic difference between the SIGNAL at applied load and the SIGNAL at MINIMUM LOAD.
– The resistance of the LOAD CELL circuit measured at the SIGNAL terminals with no load applied and with the excitation terminals open-circuited.
– The axis along which the LOAD CELL is designed to be loaded.
– The OUTPUT corresponding to CAPACITY, equal to the algebraic difference between the SIGNAL at (MINIMUM LOAD + CAPACITY) and the SIGNAL at MINIMUM LOAD.
– The smallest change in load which produces a detectable change in the SIGNAL.
– Electrical simulation of OUTPUT by connection of shunt resistors of known values at appropriate points in the circuitry.
– Any load at the point of AXIAL LOAD application acting at 90° to the PRIMARY AXIS.
– The absolute level of the measurable quantity into which a force input is converted.
– Another name for RATED OUTPUT.
– The band of maximum deviations of the ascending and descending calibration points from a best fit line through zero OUTPUT. It includes the effects of NONLINEARITY, HYSTERESIS, and non-return to MINIMUM LOAD. Normally expressed in units of %FS.
– A computed value for OUTPUT at CAPACITY derived from a line best fit to the actual ascending and descending calibration points and through zero OUTPUT.
– The algebraic difference between the RATED OUTPUT in tension and the average of the absolute values of RATED OUTPUT in tension and RATED OUTPUT in compression. Normally expressed in units of %RO.
– The change in OUTPUT due to a change in AMBIENT TEMPERATURE. Normally expressed as the slope of a chord spanning the COMPENSATED TEMPERATURE RANGE and in units of %/°F or %/100°F.
– The change in ZERO BALANCE due to a change in AMBIENT TEMPERATURE. Normally expressed as the slope of a chord spanning the COMPENSATED TEMPERATURE RANGE and in units of %RO/°F or %RO/100°F.
– The range of temperature over which the LOAD CELL is compensated to maintain OUTPUT and ZERO BALANCE within specified limits.
– The extremes of AMBIENT TEMPERATURE within which the LOAD CELL will operate without permanent adverse change to any of its performance characteristics.
– Another name for ZERO FLOAT.
– The SIGNAL of the LOAD CELL in the NO LOAD condition.
– Another name for ZERO FLOAT.
– The shift in ZERO BALANCE resulting from a complete cycle of equal tension and compression loads. Normally expressed in units of %FS and usually characterized at FS = CAPACITY.
– The degree to which ZERO BALANCE is maintained over a specified period of time with all environmental conditions, loading history, and other variables remaining constant.
– force applied in one direction, tension or compression, from 0 to 100, constant for an extended period of time
– loads that vary in both force and direction
– multiple cycles, 100% compression to 100% tension load
– a mechanical solution that protects a load cell from exceeding forces
– used to modify the signal to the type of output required, including;4-20mA, ±5V, ±10V, 0-5V, and 0-10V
– a load cell with electronic identification inside, including sensor information and calibration data
Interface offers a complete line of instrumentation to provide you with exactly the information you need, including: indicators, signal conditioners and PC interface modules with USB and software options.
The creation of this instructional guide, Interface Load Cell Field Guide, was driven by a statement in Interface’s mission to always go above and beyond. We believe this informative reference is a helpful resource from the company that is recognized as pioneers in force measurement and load cell design and manufacturing. Our team of the most innovative load cell engineer’s best understand their design, capabilities, multitude of uses, and capacities. They are eager to share their knowledge and collective expertise to help other engineers and designers with load cell fundamentals to help make better force measurement decisions.
Interface’s Load Cell Field Guide was first published in 2014. As a result, we have heard how much the book helps fellow engineers around the world learn about the intricacies of load cell design and about some of the many applications of load cells in force measurement. In our new edition, we updated essential information to provide more value to load cell users and force measurement enthusiasts.
Interface has been designing and manufacturing load cells since our founding in 1968. We are extremely proud of our history and our products. As we move into our 2nd 50, we continue our commitment to provide the absolute best in force measurement solutions.
We know our customers rely on our products to make their products perform at their best. Our purpose is to enable innovation across all industries. Innovation that improves people’s lives and keeps them safe.
This means quality in products and production are cornerstones for our business. Interface is an integrated manufacturing operation. Whether we are making standard off the shelf Interface LowProfile load cells, modified minis, or our custom designed torque or wireless solutions, we control the process from the initial customer quote until the products ship out the door. We believe that beyond a great design, the process and control of the process are what enables a load cell to have the accuracy and dependability of an Interface Load Cell.
The load cell starts in our factory as a raw piece of steel, aluminum, or other metal that is then machined, gaged, wired, finished, and finally calibrated. As you can understand from this book, strain gages are what make a load cell a load cell. How they are made and how they are handled is critical to the operation and accuracy of a load cell. That is why we chose to be one of the only load cell companies in the world that manufactures its own strain gages. This guide is also available on Amazon, if you prefer the printed copy.
Frequently, customers want to use a load cell as an element in the physical structure of a machine or assembly. Therefore, they would like to know how the cell would react to the forces developed during the assembly and operation of the machine.
For the other parts of such a machine, made from stock materials, the designer can look up their physical characteristics (such as thermal expansion, hardness, and stiffness) in handbooks and determine the interactions of his parts based on his design. However, since a load cell is built on a flexure, which is a complex machined part whose details are unknown to the customer, its reaction to forces will be difficult for the customer to determine.
It is a useful exercise to consider how a simple flexure responds to loads applied in different directions. Figure 14 shows examples of a simple flexure, made by grinding a cylindrical groove into both sides of a piece of steel stock. Variations of this idea are used extensively in machines and test stands to isolate load cells from side loads. In this example, the simple flexure represents a member in a machine design, not an actual load cell.
The thin section of the simple flexure acts as a virtual frictionless bearing having a small rotational spring constant. Therefore, the spring constant of the material may have to be measured and factored into the response characteristics of the machine.
If we apply a tensile force, Fn or a compressive force, Fe, to the flexure at an angle off of its centerline, the flexure will be distorted sideways by the vector component, FTX or Fex, as shown by the dotted outline. Although the results looks quite similar for both cases, they are drastically different.
In the tensiIe case in Figure 14, the flexure tends to bend into alignment with the off-axis force and the flexure assumes an equilibrium position safely, even under considerable tension.
In the compressive case, the flexure’s reaction, as shown in Figure 15, can be highly destructive, even though the applied force is exactly the same magnitude and is applied along the same line of action as the tensile force, because the flexure bends away from the line of action of the applied force. This tends to increase the side force, F’ex, with the result that the flexure bends even more. If the side force exceeds the ability of the flexure to resist the turning motion, the flexure will continue to bend and will ultimately fail. Thus, the failure mode in compression is bending collapse, and will occur at a much lower force than can be safely applied in tension.
The lesson to be learned from this example is that extreme caution must be applied when designing compressive load cell applications using columnar structures. Slight misalignments can be magnified by the motion of the column under compressive loading, and the result can range from measurement errors to complete failure of the structure.
The previous example demonstrates one of the major advantages of the Interface Low Profile cell design. Since the cell is so short in relation to its diameter, it does not behave like a column cell under compressive loading. It is much more tolerant of misaligned loading than a column cell.
The stiffness of any load cell along its primary axis, the normal measurement axis, can be calculated easily, given the rated capacity of the cell and its deflection at rated load. Load cell deflection data can be found in the Interface Catalog.
Keep in mind that these values are typical, but are not controlled specifications for the load cells. In general, the deflections are characteristics of the flexure design, the flexure material, the gage factors and the final calibration of the cell. These parameters are each individually controlled, but the cumulative effect may have some variability.
Using the SSM-100 flexure in Figure 16 as an example, the stiffness in the “Z” direction (the primary axis) can be calculated as follows:
Where:
Stiffness on primary axis
Rated Capacity
Deflection at Rated Output
For the SSM-100:
This type of calculation is true for any linear load cell on its primary axis. In contrast, the stiffnesses of the “Xli and “Y” axes are much more complicated to determine theoretically, and they are not usually of interest for users of Mini Cells, for the simple reason that the response of the cells on those two axes is not controlled as it is for the Low Profile series. For Mini Cells, it is always advisable to avoid the application of side loads as much as possible, because the coupling of off-axis loads into the primary axis output can introduce errors into the measurements.
For example, application of the side load, Fx, causes the gages at “AI! to see tension, and the gages at “B” to see compression. If the flexures at “A” and liB” were identical and the gage factors of the gages at “A” and liBII were matched, we would expect the output of the cell to cancel the effect of the side load. However, since the SSM series is a low-cost utility cell which is typically used in applications having low side loads, the extra cost to the customer of balancing out the side load sensitivity is usually not justifiable.
The correct solution where side loads or moment loads may occur is to uncouple the load cell from those extraneous forces by the use of a rod end bearing at one or both of the ends of the load cell.
For example, Figure 17 shows a typical load cell installation for weight of a barrel of fuel sitting on a weigh pan, in order to weigh the fuel used in engine tests.
A clevis is mounted firmly to the support beam by its stud. The rod end bearing is free to rotate around the axis of its support pin, and can also move about ±10 degrees in rotation both in and out of the page and around the primary axis of the load cell. These freedoms of motion ensure that the tension load stays on the same centerline as the load cell’s primary axis even if the load is not properly centered on the weigh pan.
Note that the nameplate on the load cell reads upside down, because the dead end of the cell must be mounted to the support end of the system.
Frequently, a load cell will be used in a situation where a light load, such as a weigh pan or small test fixture will be attached to the live end of the cell. The user would like to know how quickly the cell will respond to a change in loading. By connecting the output of a load cell to an oscilloscope and running a simple test, we can learn some facts about the dynamic response of the cell. If we firmly mount the cell on a massive block and then tap the cell’s active end very lightly with a tiny hammer, we will see a damped sine wave train (a series of sine waves which progressively decrease to zero).
Use extreme caution when applying impact to a load cell. The force levels can damage the cell, even for very short intervals.
The frequency (number of cycles occurring in one second) of the vibration can be determined by measuring the time (T) of one complete cycle, from one positive-going zero crossing to the next. One cycle is indicated on the oscilloscope picture in Figure 18 by the bold trace line. Knowing the period (time for one cycle), we can calculate “fo” (the natural frequency of free oscillation of the load cell) from the formula:
Where:
natural frequency
time for one cycle
The natural frequency of a load cell is of interest, because we can use its value to estimate the dynamic response of the load cell in a lightly loaded system.
Natural frequencies are typical values, but are not a controlled specification. They are given in the Interface catalog only as an assistance to the user.
The equivalent spring-mass system of a load cell is shown in Figure 190 The mass, mb corresponds to the mass of the live end of the cell, from the attachment point to the thin sections of the flexure. The spring, having spring constant K, represents the spring rate of the thin measurement section of the flexure. The mass, m2, represents the added mass of any fixtures which are attached to the live end of the load cell.
Figure 20 relates these theoretical masses to the actual masses in a real load cell system. Note that the spring constant, K, occurs on the dividing line at the thin section of the flexure.
Natural frequency is a basic parameter, the result of the design of the load cell, so the user must understand that the addition of any mass on the active end of the load cell will have the effect of lowering the total system’s natural frequency. For example, we can imagine pulling down slightly on the mass m1, in Figure 19, and then letting go. The mass will oscillate up and down at a frequency determined by the spring constant, K, and the mass of m1. In fact, the oscillations will damp out as time progresses in much the same way as in Figure 18.
If we now bolt the mass m2 on m1, the increased mass loading will lower the natural frequency of the spring-mass system. Fortunately, if we know the masses of m1 and m2, and the natural frequency of the original spring-mass combination, we can calculate the amount that the natural frequency will be lowered by the addition of m2, according to the formula:
Where:
system natural frequency
load cell natural frequency
load cell live end mass
added fixture mass
To an electrical or electronic engineer, the static calibration is a “DC” parameter, whereas the dynamic response is an “AC” parameter. This is represented in Figure 21, where the DC calibration is shown on the factory calibration certificate, and users would like to know what the response of the cell will be at some driving frequency they will be using in their tests.
Note the equal spacing of the “Frequency” and “Output” grid lines on the graph in Figure 21. Both of these are logarithmic functions; that is, they represent a factor of 10 from one grid line to the next. For example, “0 db” means “no change”; “+20 db” means “10 times as much as 0 db”; “–20 db” means “1/10 as much as 0 db”; “–40 db” means “1/100 as much as “0 db.”
By using logarithmic scaling, we can show a larger range of values, and the more common characteristics turn out to be straight lines on the graph. For example, the dashed line shows the general slope of the response curve above the natural frequency. If we continued the graph down and off to the right, the response would become asymptotic (closer and closer) to the dashed straight line.
The curve in Figure 21 is provided only to portray the typical response of a lightly loaded load cell under optimum conditions. In most installations, the resonances in the attaching fixtures, test frame, driving mechanism and UUT (unit under test) will predominate over the load cell’s response.
In cases where the load cell is mechanically tightly coupled into a system where the masses of the components are significantly heavier than the load cell’s own mass, the load cell tends more to act like a simple spring which connects the driving element to the driven element in the system.
The problem for the system designer becomes one of analyzing the masses in the system and their interaction with the very stiff spring constant of the load cell. There is no direct correlation between the load cell’s unloaded natural frequency and the heavily loaded resonances which will be seen in the user’s system.
Almost everyone has bounced a basketball and noticed that the period (time between cycles) is shorter when the ball is bounced closer to the floor. Anyone who has played a pinball machine has seen the ball rattling back and forth between two of the metal posts; the closer the posts get to the diameter of the ball, the faster the ball will rattle. Both of these resonance effects are driven by the same elements: a mass, a free gap, and a springy contact which reverses the direction of travel.
The frequency of oscillation is proportional to the stiffness of the restoring force, and inversely proportional both to the size of the gap and to the mass. This same resonance effect can be found in many machines, and the buildup of oscillations can damage the machine during normal operation.
For example, in Figure 23 a dynamometer is used to measure the horsepower of a gasoline engine. The engine under test drives a water brake whose output shaft is connected to a radius arm. The arm is free to rotate, but is constrained by the load cell. Knowing the RPM of the engine, the force on the load cell, and the length of the radius arm, we can calculate the horsepower of the engine.
If we look at the detail of the clearance between the ball of the rod end bearing and the sleeve of the rod end bearing in Figure 23, we will find a clearance dimension, liD,” because of the difference in size of the ball and its constraining sleeve. The sum of the two ball clearances, plus any other looseness in the system, will be the total IIgapII which can cause a contact resonance with the mass of the radius arm and the spring rate of the load cell.
As the engine speed is increased, we may find a certain RPM at which the rate of firing of the engine’s cylinders matches the contact resonance frequency of the dynamometer. If we hold that RPM, magnification (multiplication of the forces) will occur, a contact oscillation will build up, and impact forces of ten or more times the average force could easily be imposed on the load cell.
This effect will be more pronounced when testing a one-cylinder lawn mower engine than when testing an eight cylinder auto engine, because the firing impulses are smoothed out as they overlap in the auto engine. In general, raising the resonant frequency will improve the dynamic response of the dynamometer.
The effect of contact resonance can be minimized by:
Any transducer which depends upon the deflection of a metal for its operation, such as a load cell, torque transducer or pressure transducer, retains a history of its previous loadings. This effect occurs because the minute motions of the crystalline structure of the metal, small as they are, actually have a frictional component which shows up as hysteresis (non-repeating of measurements which are taken from different directions).
Prior to the calibration run, the history can be swept out of the load cell by the application of three loadings, from zero to a load which exceeds the highest load in the calibration run. Usually, at least one load of 1300/0 to 140% of the Rated Capacity is applied, to allow the proper setting and jamming of the test fixtures into the load cell.
If the load cell is conditioned and the loadings are properly done, a curve having the characteristics of A-B-C-D-E-F-G-H-I-J-A, as in Figure 24, will be obtained. The points will all fall onto a smooth curve, and the curve will be closed on the return to zero. Furthermore, if the test is repeated and the loadings are properly done, the corresponding points between the first and second runs will fall very close to each other, demonstrating the repeatability of the measurements.
Whenever a calibration run yields results which don’t have a smooth curve, don’t repeat well, or don’t return to zero, the test setup or loading procedure should be the first place to check.
For example, Figure 24 shows the result of the application of loads where the operator was not careful when the 60% load was applied. If the weight was dropped slightly onto the loading rack and applied an impact of 80% load and then returned to the 600/0 point, the load cell would be operating on a minor hysteresis loop which would end up at point “P” instead of at point “D.” Continuing the test, the 80% point would end up at “R,” and the 1000/0 point would end up at “S.” The descending points would all fall above the correct points, and the return to zero would not be closed.
The same type of error can occur on a hydraulic test frame if the operator overshoots the correct setting and then leaks back the pressure to the correct point. The only recourse for impacting or overshooting is to recondition the cell and start the test over.
Load cells are routinely conditioned in one mode (either tension or compression), and then calibrated in that mode. If a calibration in the opposite mode is also required, the cell is first conditioned in that mode prior to the second calibration. Thus, the calibration data reflects the operation of the cell only when it is conditioned in the mode in question.
For this reason, it is important to determine the test protocol (the sequence of load applications) which the customer is planning to use, before a rational discussion of the possible sources of error can occur. In many cases, a special factory acceptance must be devised to ensure that the user’s requirements will be met.
For very stringent applications, users are generally able to correct their test data for the nonlinearity of the load cell, thus removing a substantial amount of the total error. If they are unable to do so, nonlinearity will be part of their error budget.
Nonrepeatability is essentially a function of the resolution and stability of the user’s signal conditioning electronics. Load cells typically have nonrepeatability which is better than the load frames, fixtures and electronics used to measure it.
The remaining source of error, hysteresis, is highly dependent on the loading sequence in the user’s test protocol. In many cases, it is possible to optimize the test protocol so as to minimize the introduction of unwanted hysteresis into the measurements.
However, there are cases where users are constrained, either by an external customer requirement or by an internal product specification, to operate a load cell in an undefined way which will result in unknown hysteresis effects. In this event, the user will have to accept the worst case hysteresis as an operating specification.
Also, some cells must be operated in both modes (tension and compression) during their normal use cycle without being able to recondition the cell before changing modes. This results in a condition called toggle . (non-return to zero after looping through both modes). In normal factory output, the magnitude of toggle is a broad range where the worst case is approximately equal to or ~light1y larger than hysteresis, depending on the load cell’s flexure material and capacity.
Fortunately, there are several solutions to the toggle problem:
All on-axis loadings generate some level, no matter how small, of off-axis extraneous components. The amount of this extraneous loading is a function of the tolerancing of the parts in the design of the machine or load frame, the precision with which the components are manufactured, the care with which the elements of the machine are aligned during assembly, the rigidity of the load-bearing parts, and the adequacy of the attaching hardware.
The user can opt to design the system so as to eliminate or reduce off-axis loading on the load cells, even if the structure suffers distortion under load. In tension mode, this is possible by the use of rod end bearings with clevises.
Where the load cell can be kept separate from the structure of the test frame, it can be used in compression mode, which almost eliminates the application of off axis load components to the cell. However, in no case can off-axis loads be completely eliminated, because the deflection of load carrying members will always occur, and there will always be a certain amount of friction between the load button and the loading plate which can transmit side loads into the cell.
When in doubt, the Low Profile cell will always be the cell of choice unless the overall system error budget allows a generous margin for extraneous loads.
In high-precision test applications, a rigid structure with low extraneous loading can be achieved by the use of ground flexures to build the measurement frame. Of course, this requires precision machining and assembly of the frame, at considerable cost.
One serious effect of off-axis loading is the reduction of the cell’s overload capacity. The typical 150% overload rating on a standard load cell or the 300% overload rating on a fatigue-rated cell is the allowed load on the primary axis, without any side loads, moments or torques applied to the cell concurrently. This is because the off-axis vectors will add with the on-axis load vector, and the vector sum can cause an overload condition in one or more of the gaged areas in the flexure.
To find the allowed on-axis overload capacity when the extraneous loads are known, compute the on-axis component of the extraneous loads and algebraically subtract them from the rated overload capacity, being careful to keep in mind in which mode (tension or compression) the cell is being loaded.
Neophytes in the use of load cells frequently destroy one before an old-timer has a chance to warn them about impact loads. We would all wish that a load cell could absorb at least a very short impact without damage, but the reality is that, if the live end of the cell moves more than 150% of the full capacity deflection in relation to the dead end, the cell could be overloaded, no matter how short the interval over which the overload occurs.
In Panel 1 of the example in Figure 24, a steel ball of mass “m” is dropped from height “S” onto the live end of the load cell. During the fall, the ball is accelerated by gravity and has achieved a velocity “v” by the instant it makes contact with the surface of the cell.
In Panel 2, the velocity of the ball will be completely stopped, and in Panel 3 the direction of the ball will be reversed. All this must happen in the distance it takes for the load cell to reach the rated overload capacity, or the cell may be damaged.
In the example shown, we have picked a cell which can deflect a maximum of 0.002” before being overloaded. In order for the ball to be completely stopped in such a short distance, the cell must exert a tremendous force on the ball. If the ball weighs one pound and it is dropped one foot onto the cell, the graph of Figure 26 tells us that the cell will receive an impact of 6,000 lbf (It is assumed that the mass of the ball is much larger than the mass of the live end of the load cell, which is usually the case.)
The scaling of the graph can be modified mentally by keeping in mind that the impact varies directly with the mass and with the square of the distance dropped.
Load cells are constructed using electric resistance metal foil strain gages bonded to an elastic flexure element. The load cell is a passive analog device with continuous resolution limited ultimately by noise, due to electron motion on the order of 10-9 volts (1 nanovolt). Therefore, practically speaking, resolution is limited by the type and quality of the electronic instrumentation used, rather than by the load cell itself. Many reasonably priced instruments can resolve 0.8 to 1.0 microvolt/count as a minimum signal level.
For example, consider a load cell with Rated Output of 3mV/V. Assume that 10VDC excitation is used. At Rated Output, the signal level produced would be:
3mV/V x 10V = 30 mV
If the indicating instrument can resolve 1 microvolt in the rightmost digit of the display, then:
Resolution = 1 µvolt/30 mV
= 1 µvolt/30,000 µvolt
= 0.000033, fraction of Rated Output
= 0.0033 % of Rated Output
If, for example, an MB-5 (5 lbf Rated Capacity) load cell were being used, the resolution in pounds could be calculated as:
Resolution = 5 lbf x 0.000033
= 0.00017 lbf
If an instrument capable of 0.5 microvolt resolution were used, the resolution would be approximately 1 part in 60,000 or 0.000083 pounds for the 5 pound capacity cell. Maximum resolution may be limited by the instrument to the total number of counts that can be displayed.
Another typical example would be the case where only a portion of the range of the load cell is to be used. If the maximum load on the MB-5 were to be 3 pounds, then the output would be:
3 mV/V x 3 lbf / 5 lbf = 1.8 mV/V
Using 10V excitation provides a signal of 18 mV output for 3 pounds input. If the instrument displays is to display 30,000 counts a signal strength of
18 mV / 30,000 counts = 0.6 microvolt/count
results in a display of 0.00015 pound/count resolution. Of course, the instrument must have a sensitivity of at least 0.6 µvolt/count for this example.
It can be seen from the above examples that the sensitivity and stability of the electronic instrumentation is critical, when high resolution is required. High electronic gain alone will not achieve good results if the zero stability or gain stability is poor because the readings will drift with time or temperature changes.
Also, keep in mind that excessive resolution can be detrimental in situations where the stability of the applied force is low, as in some hydraulic systems.
Generally, it is desired to read physical units instead of counts. Most instruments provide a count-by feature of 1, 2, 5 or 10 to facilitate this. For the above example, an instrument could be set up to read 30,000 counts by 2 for the 3 pound load, providing resolution of 0.0002 lbf Premium instruments are available that offer as good as 0.001µvolt/count.
We have capacities ranging from 1 lbf / 500 gf to 2 million lbf / 9,000 kN. Our facility produces them in several shapes and sizes. Models include pancake load cell and donut load cell in our LowProfile® load cell and thru-hole load cell. Additionally, our canister, rod end, downhole, column, coil tubing, load buttons, and load washers all use our proprietary alloy strain gages. This helps us produce the most accurate and reliable data possible in test and measurment. With the wide variety of load cell specs in stock, most customers are able to use an off-the-shelf application. However, our engineers can also work with you to design a custom load cell to fit your exact needs. Contact us so that we can help you find a solution that fits your requirements.
The testing of materials and complex assemblies is such a vast field that it is impossible to cover all aspects of it completely in this manual. In this section, we will give an overview of the different types of material tests and other specialized tests using force as a variable, with some examples of the most common applications.
In the determination of the force versus deflection characteristics of a raw material, a fabricated part, or an assembly, it is usually necessary to control the position and orientation of the UUT (Unit Under Test), to control the direction and magnitude of the applied force, to measure one or more displacements, and to measure any other parameter which may vary with the force or displacement. For these reasons, a large market has developed over the years for sophisticated testing machines and their associated fixtures, transducers, and signal conditioning and recording equipment.
In the typical materials testing machine shown in Figure 42, where the clamp is shown, various other fixtures can be attached to hold, or even rotate, the UUT during the test. Other transducers can be mounted to measure torque, angle, pressure or any parameter the customer is willing to pay for. It is not unusual to test for torque and linear force concurrently, and the Interface Low Profile cells are eminently suited for this because of their high rejection of extraneous loads.
With the hydraulic ram at a solid stop, the gear drive can be servo-controlled to advance the displacement at a very accurately controlled rate, to determine the time dependency of a material’s characteristics. Or, with the gear drive locked, the hydraulic ram can apply a precise force profile, as controlled by the load cell.
In general, any modern test machine is programmed and controlled by its own internal microprocessor, with facilities for accepting large volumes of control information and transmitting high rates of measured data either to a local datalogger or to a network server for further processing.
In the determination of shear strength versus compaction of soils or construction materials, the object is to determine the shear strength as the material is used at different depths underground or at different levels in the construction of a high-rise building. Usually, a special test block is designed to test a particular type of material in conformance with a specification.
The test block is designed with a rectangular hole going through it, into which the tested material is inserted. To set up for the test, the shear block is put into position in the test block so that the hole in the shear block lines up with the rectangular test hole. The material under test is then packed into the hole, up through the hole in the shear block, and almost to the top of the test block. Finally, the compaction piston is inserted, and the material is evenly pressed down to fill the hole and remove air pockets and voids.
The actual test is performed in a test frame much like a materials test machine, except that it has an additional capability to pull out the shear block while measuring the shear force and shear deflection. To perform the test, the compaction force is first applied on the top of the compaction piston by a compression load cell, and then the tension shear force is applied to the shear block by another load cell. The test is repeated for a range of compaction forces, and the output from the test is a table of figures or a graph of shear force versus compaction force.
A common test for adhesives, adhesive-coated tapes, and paints is the peel test.
The test parameters are usually detailed in a government or industry specification, and the rate of pull is most often closely controlled. Adhesive-backed tapes are tested this way. Also, paint adhesion is tested by applying the paint according to instructions, applying a specified adhesive-backed tape to the painted surface, and then pulling the tape off in a specified way.
There are literally thousands of adhesives and bonding agents which are used to assemble parts into assemblies. In addition to their bonding characteristics, they may be required to have a certain elasticity, resistance to chemicals, electrical conductivity, temperature coefficient, or other controlled parameter.
In addition to the general-purpose shear test machines on the market, many testers are designed and constructed in-house to perform specific tests on unique assemblies.
The design of a shear tester is relatively straightforward, as long as the following conditions are met:
Many industry and government specifications require testing the components of a system at many times the rated or nameplate loading, where the failure of the component could result in costly damage to equipment or injury to personnel.
The most sensitive product liability area for load cell manufacturers is the use of a load cell in tension on a crane which lifts loads where it is possible that a person could be under the load, even by mistake. Proof testing in this case usually requires that the equipment be proof tested at five times its rating. Obviously, a tension load cell could never survive such a test. Interface never recommends using a tension load cell in this type of application.
The most straightforward solution, where it is necessary to measure the load in a tension cable subject to safety considerations is to enclose the load cell in a compression cage, which converts tension into compression. The compression cell is trapped between the two plates. Thus, the load cell’s only overload failure mode is in compression, which allows a motion of only 0.001” to 0.010” before the load cell becomes solid. Even if the load cell is totally destroyed, the compression cage cannot drop the load unless it fails itself. Therefore, the cage can be proof tested with a dummy load cell, or an overload protected cell, and the risk of injury to personnel is avoided.
One of the critical tests on missile assemblies is the determination of the center of gravity, because variations in the weight distribution in a missile can have a disastrous effect on its flight stability.
The test stand shown in Figure 47 typifies the elements which need to be addressed to optimize the test.
The designer who promotes a three-cell system may meet with some opposition from engineers whose minds are used to working in an orthogonal (right angled) reference system. However, the mechanical headaches associated with the shimming of a four-cell system and readjusting it when the temperature varies are worth the extra effort to solve the equations for a triangular system.
For example, if the CG (center of gravity) is supposed to be at the exact center of the triangular pattern of the load cells, the diagram in Figure 48 shows the load cells at ~ B, and C all measuring exactly the same loads cx, P, and y. When those load vectors are plotted as distances from their respective opposite sides (which are the fulcrums against which the vectors operate), we find that they coincide at the CG, at the exact centroid of the triangular load cell pattern.
This means that the CG is exactly where it should be, and it also gives us fair assurance that the system has been properly calibrated.
However, if the CG is mislocated in the missile, as in Figure 49, the vectors will define a different set of distances from their respective fulcrums. When we measure the vector cx from the baseline BC, we construct line be parallel to the baseline BC. In the same manner, we construct line ae at distance from baseline AC. The intersection of lines ae and be defines the CG point.
The question then arises, “How did we find the CG without using line ab?” The answer is, “Any two of the lines could define the CG, because the data from all three cells was used to define the two lines, and the intersection of two lines defines a point. “
The position of the third line is a redundant check, and is a nice way of checking the accuracy of the measurement. If the third line (whichever one we choose) does not go through the same point as the intersection of the first two lines, we need to check our test system and find the error, because all three lines should agree on the location of the eG. In Figure 49, the CG is mislocated, but all three lines agree on the intersection point. Thus, the test is good, but the CG is mislocated in the missile.
In most applications it is difficult, if not impossible, to calculate or even estimate the effect of misalignments on the precision of a force measurement system. Moment sensitivity introduces errors into force measurements whenever forces cannot be applied precisely on-axis.
The Interface Low Profile design provides optimum resistance to extraneous loads to insure maximum operation life and minimize reading errors. The above chart tabulates maximum allowable extraneous loads that may be applied singularly without electrical or mechanical damage to the cell and the maximum error that can be expected from side forces or bending moments. Several loads can be tolerated simultaneously if the total combined load is not more than 100% of the allowable maximum extraneous load.
Only Interface guarantees maximum extraneous load error and physically adjusts every load cell. The Interface 1200 Series cells have eccentric load sensitivity less than ±0.25% of reading per inch, and the 1000, 1100, and 1600 Series are further adjusted to come in at less than ±0.1% of reading per inch. Most competing load cells will have extraneous load error 10 times higher (or even more) than with a superior Interface load cell.
Compression cells are widely used for weighing applications because they are less expensive and in some cases have slightly lower errors. Figure 27 shows a typical application. The load cell with base is mounted on the stud which is permanently affixed in the bottom plate. This gives the cell added protection against any uneven surface under the bottom plate which might affect the calibration of the cell.
The load cell’s load button is hard anodized or heat treated to ensure a hard surface. The load bearing surface of the top plate must be heat treated to increase its hardness. Cold rolled steel or similar material is not appropriate, because the surface will soon gall and become useless. Also, the finish of both the top plate’s bearing surface and load cell’s load button should have 32 µinch or smoother surface roughness to ensure that galling will not occur.
The configuration of Figure 27 is widely used because the cell with base can be removed as a complete assembly by screwing it off of the bottom plate’s stud. When it is replaced, the original factory calibration of the new cell can be preserved, because the base protects the load cell against any unevenness in the surface facing the bottom of the base.
The configuration of Figure 28 is used in situations where the bottom surface of the hopper leg which bears on the load cell/bottom plate assembly can be machined flat and smooth. This allows the load cell to be mounted directly on the bottom plate, without an intervening base, thus saving the cost of a base. Although conceptually simpler, this configuration requires that the bottom plate be installed at the factory so that the assembly can be calibrated. This configuration also protects the diaphragm surface of the load cell from being subjected to standing water in installations having water misting or splashing.
The majority of compression cell applications are multiple-cell installations. The number of cells may run anywhere from 3 cells on a simple weighing platform to 16 cells on a long truck scale.
In every case, the accuracy and repeatability of the system will be improved by following these simple rules:
When designing the mechanical mounting of the cells in a multiple-cell system, provisions should be made for the leveling adjustment necessary to equalize the loading of the cells among all the “corners” of the system. (In this context, all the cells in a multicell system are called “comers,” even though some of them may be on sides, between corners.) It is advantageous that all the cells operate at the same point on their operating curves, by being equally loaded, in order to achieve maximum system accuracy.
Everyone has had the experience of sitting on a four-legged chair which has one slightly short leg, and getting the feeling of rocking back and forth with one or the other leg always off the floor. Although we think that our weight is being carried by three of the four legs, in truth almost our whole weight is sometimes on only two of the legs. The same effect can be seen on a multiple-cell system which has been improperly shimmed.
In an improperly equalized four-cell system, it is possible that the total load could be carried momentarily by two diagonally opposite load cells, which would be almost certain to overload the cells.
The “rocking chair” effect will be more or less pronounced, depending on the stiffness of the framework or structure which transmits the load to the cells.
For example, we can construct a very stiff system by making a tank out of a thick-walled steel pipe four feet in diameter, with a flat bottom welded inside it part way up from the bottom, as in Figure 30. The bottom edge of the pipe is prepared by having hard inserts welded into it to match the locations of the load buttons on the load cells, and the inserts are carefully ground to a planar surface. The four load cells are mounted on a very thick, stiff steel plate which has been ground as flat as humanly possible.
As the pipe is slowly and carefully lowered onto the cells, we find to our dismay that two diagonally opposite cells are taking much more load than the other two cells. This is happening because the full scale deflection of the load cells is only a few thousandths of an inch, and it is too costly, if not impossible, to grind the surfaces of the plate and the tank that flat over such a large span to that close a tolerance.
If we had any intention of shimming the cells to equalize the loading, we would need to use shims that are only about 1/5 the thickness of a piece of paper. Such a task would take days to accomplish. In addition, distortion of the tank by temperature gradients (uneven changes in temperature) in the tank when the sun shines on it or when hot liquid is pumped into it would introduce dramatic changes in the careful job of shimming which we had just finished.
The important lesson to be learned from this example is that there needs to be some flexibility built into the design of the tank structure to make the shimming job easier and to reduce the effect on the cell loading caused by temperature gradients distorting the tank. Figure 31 simulates a springy system by actually picturing springs under the legs, which makes it easier to visualize how a springy frame alleviates the shimming problem.
We can now calculate the effect of the addition of a shim which is 0.002” thick. Let’s assume a 10,000 lbf load cell with a deflection of 0.002” at full capacity, which gives it a stiffness of 5 million pounds per inch.
In the “stiff” case of Figure 30, adding or removing one shim only 0.002” thick would change the load on that cell by 5,000 lbf. Thus, it would be very difficult to adjust the loading on the cell in increments of 5% of full capacity. (The reader is left with the problem of figuring out why the change in loading is only 1/2 of the “expected” value.)
Now, let’s assume that the springs in Figure 31 have been chosen to have a stiffness of 50,000 pounds per inch, 1/100th of the stiffness of the load cells. When we first lower the frame onto the cells, the springs will alleviate much of the uneven loading on the cells. In addition, as we check the cells’ outputs, we find that the addition of a shim of 0.002” thickness raises the loading on that cell by 50 Ibf, well within the equalization increment of 5% of full capacity which we were shooting for.
Equalizing a tension system is a much easier task than shimming a compression system. The load cells will all be moment protected, either by the use of rod end bearings and clevises or by using flexible cable assemblies on each cell. It is then necessary only to insert a turnbuckle in one of the supports on a four-cell system, two of the supports in a five-cell system, or three of the supports in a six-cell system. Since one-, two-, or three cell systems do not need physical shimming adjustment, they are obviously much easier to install, and are hardly affected by distortions due to temperature gradients in the support framework.
After the cells have all been equalized, an electrical comer adjustment will be needed on most systems unless it has already been done at the factory.
Do not change any adjustments on a system which has already been calibrated at the factory. The factory calibration will be lost.
Corner adjustment is accomplished as follows:
In the same way that a load cell can have moment sensitivity (output variation for off-axis loads), a weigh platform can respond differently for loads which are not exactly on the center of the platform. In the case of Figure 32, where the three load cells are equally spaced around the bolt circle with radius “R,” if the outputs of the cells are corner adjusted properly, the weight indication of the platform will be the same for any location of a test weight. This fact would seem to be intuitively true, simply because of the symmetry of the load cell layout.
But, when we propose the layout of Figure 33, the lack of rotational symmetry strains our intuition, and we may struggle with the concept that the only criterion for a successful weigh platform is that the cells are corner adjusted. However, strict mathematical analysis of either system yields the same answer: corner adjustment alone is sufficient.
There may be a functionally logical reason for the arrangement of Figure 33, or even Figure 34. In many cases, the load may be applied from a particular edge or a motor/gear assembly may be mounted off-center, and the concentration of cells closer together tends to distribute the load between the three cells more evenly.
The dimensions in Figure 34 are correct for an evenly loaded conveyor frame where the loads are dumped onto frame at the left end, on the line connecting the two cells. This arrangement gives more margin to protect the cells from overload. Incidentally, the load is equally divided among the cells when there is no product on the conveyor (tare condition) or the load is at the center mark of the conveyor.
The reader may have noticed that all the examples in this section use only three cells. Most applications can be solved by a three-cell arrangement, unless the designer failed to consult with the load cell supplier early enough in the design phase of the project and ended up with a hopper or tank structure which was driven by the idea of a square section with four legs. Given the difficulty of equalizing or shimming a four-cell system and the effects of temperature gradients on the measurements, eliminating one cell is sometimes a major improvement in the design.
Many applications can be easily implemented with either a two-cell or a one-cell arrangement, provided the justification criteria are met. This section outlines how these cost saving systems can be specified and designed.
The simplest one-cell system is the tension cell mounted through rod end bearings and clevises as shown in Figure 17. If the cell is properly oriented with the dead end going to the support, the only other major consideration is the elimination or reduction of possible parallel load paths, which are covered in the section on “Parallel Load Paths.”
The high-impact platform of Figure 35 combines the low cost of a one-cell system with the ability to withstand the impact of the rough treatment from handlers of large drums, LPG tanks, etc. The disadvantage of the system is that the CG (center of gravity) of the load must be placed on the mark for the calibration of the system to hold true. This can be accomplished by positioning the fences so that the CG of the particular product is located properly when the drum is shoved up against the fences. Two or more products which have different drum diameters can be accommodated by having movable fences with stop pins to position them correctly for each load or by using the multiple-cell capability in the 9840 Smart Indicator by setting up a scale factor for each drum diameter.
The actual load at the CG of the drum will be factored by the lever arm:
Where:
Indicated Load
True Load
Distance from load CG to Load Cell
Distance from load CG to Hinge Line
This concept has been used successfully for systems handling drums in the range of 180 to 400 pounds. For stubborn impact cases, the load cell can be configured with overload protection or the overload protection can be built into the platform as shown in Figure 36. The overload gap should be about 0.05” to 0.1 ,” and the spring constant of the flat spring should be such that a load of 110% of the load cell’s capacity will cause the platform to hit the stop block, thus shunting the excess load around the load cell.
The concept of the single-cell system works simply because the location of the center of gravity is under control. As long as the force on the primary axis of the load cell bears the same relation to the location of the CG of the load under all conditions, the scaling will be correct.
In the tension system, the CG is always directly under the load cell because the rod end bearing forces it to be there.
In the compression system, we can control the location of the CG if we know the drum diameter, by using fences. However, one additional criterion must be met: the CG must project down to the same location on the platform at any level of filling in the container. For homogeneous materials like liquids in a truly vertical cylindrical container, this will always occur. However, errors can be introduced if the platform is not level, if the container is distorted, or if any other condition causes the CG to “wander” as the container is filled.
In the two-cell system of Figure 37, the weighing rail is supported by the load cells, which are bolted to the main rails. This construction is typical of a warehouse or meat packing plant, where the product is moved around by hanging it on a hook which rides on a rail. The rail has one section which is totally supported by two load cells.
The gap at each end of the weighing rail is vee-shaped, to avoid an impact when the trolley wheel rides across the gap.
As in any system where failure of any of the components could result in damage to equipment or injury to personnel, the weighing section overlaps in such a way that it will be always be supported even if a load cell fails. The general rule on the equipment, other than the load cells, is that the system is proof tested at a load which is five times the operating specification. Naturally, the load cells would be destroyed by such a test, so the system must be designed to retain its integrity even if a load cell fails.
In the optimum design of any system using load cells, all parallel paths (load carrying paths outside the load cells) should be avoided. In cases where parallel paths carry part of the load, any variability in that load will be reflected in an equal error in the load measured by the load cells.
Especially in weighing systems, it is very difficult to avoid parallel paths completely. This is true because most hoppers have some type of power-driven device which requires a connection to the main AC power system or a piping connection for carrying the material into or out of the hopper.
Before the basic design of a weighing tank or hopper is frozen, the support structure and loading/unloading mechanisms should also be evaluated to ensure that none of the parallel paths (pipes, conduit and check rods) will introduce excessive errors into the weighing system.
For example, Figure 38 shows a vibrator (a motor with an off-center flywheel) to shake loose the powdery material in the hopper, and a screwfeeder (a long screw inside a pipe which feeds material when turned by the motor/gearbox assembly). The power wiring for both of these devices should be in flexible conduit, if allowed by the local code, and the weight of the conduit should be supported as shown to relieve the hopper from as much of the weight of the conduit as possible.
Figure 39 illustrates three types of uses for compressed air on a hopper. The upper supply injects air through jets in the side of the hopper to fluidize (mix air into a powder or slurry) to make it act like a low-viscosity fluid. The pneumatic valve is a sliding door driven by a pneumatic cylinder. Both of these should be connected to the air supply through flexible hoses, because they are parallel paths to the hopper.
The outlet pipe is connected to the hopper through a bellows, to remove the pipe as a parallel path. The connection to inject air into the outlet pipe need not be flexible, because is outside the weighing loop. The electrical wiring to control the solenoid valves is a generally a small enough gauge that it can be neglected.
At first glance it would seem that two or more load cells could simply be mounted between parallel plates to create a single assembly with increased capacity, when a larger cell is not available. Unfortunately, this is not the case, and many cells have been destroyed by hidden overloads in this situation.
In addition, unless the assembly is carefully and properly done, errors which are not obvious can be generated, and the output of the assembly could exhibit nonrepeatability, hysteresis, nonlinearity, zero balance instability, and temperature variability which are higher than would normally be seen in a single cell.
These errors would be the result of the introduction of stresses into the load cells by the process of bolting the load cells into the assembly. A single cell is carefully constructed to be free of internal stresses when at the zero balance condition.
Figure 40 illustrates what happens if the heights of all the hubs in the assembly are not exactly matched when the assembly is torqued tight.
Detail/Section A-A gives an exaggerated picture to demonstrate what happens as the stud in Cell B is tightened to close the gap created by its short hub. Cell Bls zero balance shifts in the tension direction because of the tension in the stud to close the gap.
But, that level of tension in the stud is not sufficient to provide a reliable assembly. We must continue to tighten the assembly until the surface of the upper plate and the surface of the load cell hub are flat-to-flat. This results in the introduction of a large moment torque into the load cell. Since the cell is designed to cancel moment inputs, the user may not see a shift in the output due to this moment, but some of the radial beams in the cell could be experiencing a high stress which could destroy the cell in later use.
The multi-cell assembly will be extremely sensitive to temperature gradients which are introduced by exposing one of the mounting plates to heating without heating the other plate. For example, leaving the assembly in the sun will result in differential expansion between the two plates which could very likely destroy the load cells.
In the event that it is absolutely necessary to parallel two or more cells, the following steps should be followed explicitly.
The actual force required to achieve the proper tension on the load cell during the tensioning operation will be higher than indicated on the load. cell output, because of the deflection of the upper and lower plates required to bring the load cell beyond full capacity. The plates are restrained by the parallel paths of the other load cells in the assembly.
In a multilevel tension assembly, the rated capacity should b e limited to 80% of the calculated theoretical capacity because of the unavoidable and unmeasurable residual stresses which are induced in the individual load cells by their being restrained between two stiff plates.
In a multi-cell compression system, the top plate is a ground and hardened steel plate, with a surface finish of32 µinch. It is merely resting on the load buttons of the cells. The paralleling of compression cells can be very straightforward, if these simple rules are followed:
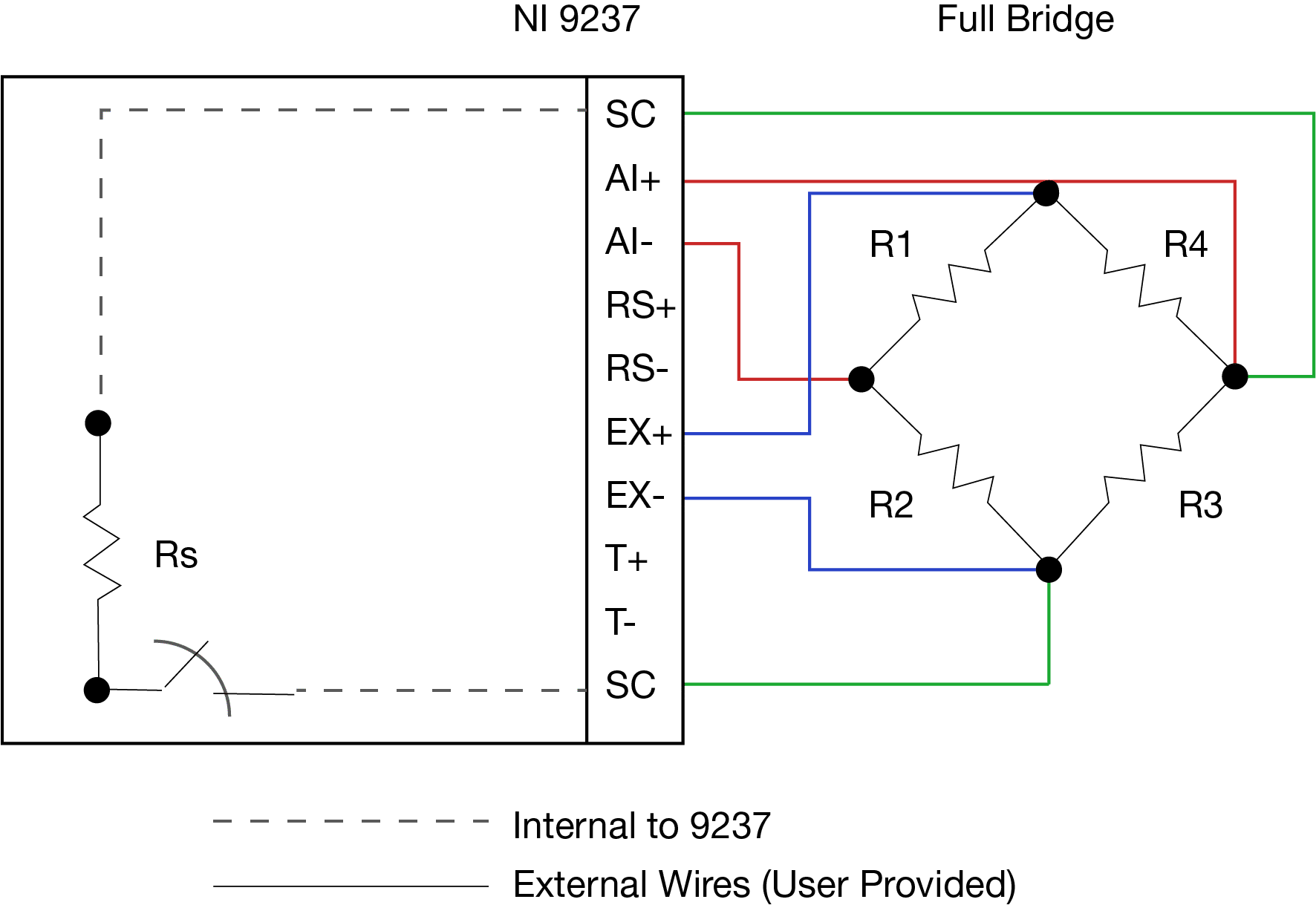
Since a strain gage load cell is a passive electrical device, there exists a simple, yet effective,
method for checking the calibration of a load cell system in the field or when a means of applying actual forces is unavailable. Inducing an electrical imbalance in the cells bridge circuit will simulate the bridge imbalance caused by the application of actual forces to the load cell. Then the system gain may be adjusted so that the system output signal or display indicates a known force on the load cell.
Be careful not to use Shunt Calibration as a substitute for actual force calibration of a system. Shunt Calibration merely supplies a known signal to the signal conditioning unit, in order to check its gain or span adjustment.
On the Calibration Certificate for each Low Profile load cell, Interface routinely supplies the value of the equivalent force resulting from connecting a specified shunt calibration resistor across one leg of the bridge. For other types of cells, Interface will supply shunt calibration values on special request.
The standard connections used by Interface for tension and compression shunt calibration are specified on the Calibration Certification for each load cell.
It is important that the standard connection be used, although a similar (but not equal) output would result from connecting to the opposite leg of the bridge. Shunt calibration is relatively insensitive to small changes in temperature, although the calibration is precisely correct only at the Lab Standard conditions noted on the load cells Calibration Certificate.
The following values of shunt resistors will cause an output of approximately 73% of Rated Output for the load cell types indicated when connected across the specified load cell terminals.
| For 4 mV/V cells: | RS-100-30K (30,000 ohms, ±0.01%) |
| For 3 mV/V cells: | RS-100-40K (40,000 ohms, ±0.01%) |
| For 2 mV/V cells: | RS-100-60K (60,000 ohms, ±0.01%) |
| For 1 mV/V cells: | RS-100-120K (120,000 ohms, ±0.01%) |
To perform a shunt calibration, use the following procedure:
The rated output (RO) of Interface load cells is the electrical output of a load or torque cell in millivolts per volt of excitation (mV/V) at the rated load. For example, the electrical voltage output of an Interface load cell with 4 mV/V at 5,000 lbs rated capacity will typically be 4 mV ± 10% or 3.6 mV/V to 4.4 mV/V. In certain applications, it could be desirable for a customer to receive cells with a tighter output tolerance. For a minimal cost, we can “standardize” the outputs within ±0.1% of the rated outputs shown in the catalog (example: 4 mV/V output would be standardized from 3.996 mV/V to 4.004 mV/V).
As a result of the trimming operation, the input resistance of the load cell may be increased. A maximum resistance on a 350 ohm bridge would not exceed 405 ohms.
Volume users who do not wish to trim their electronics for each individual load cell.
Any customer who wishes to interchange load cells without adjusting instrument.
Multiple cell installations (a weighbridge) where the cells are wired in parallel and the
outputs summed.
IEEE1451.4 specifies a table of identifying parameters that are stored in the load cell in the form of a TEDS. TEDS is a table of parameters that identify the transducer and is held in the transducer on a EEprom for interrogation by external electronics.
“Temperature Effect on Output” is defined as the change in output due to a change in ambient temperature, where output is defined as the algebraic difference between the load cell signal at applied load and the load cell signal at no load.
In strain gage based load cells, the effect is primarily due to the temperature coefficient of modules of elasticity of the force bearing metal. It is common in the industry to compensate for this effect by adding temperature sensitive resistors external to the strain gage bridge which drop the excitation voltage reaching the bridge. This has the disadvantages of adding thermal time constants to the transducer characteristic and of decreasing the output by 10%.
At Interface, external resistors are not used. Rather, by having close control over the fabrication of strain gages, the gages are made to have a temperature coefficient of gage factor which opposes the temperature coefficient of modules and thereby provides temperature compensation without loss of signal. This self temperature compensating feature is dependent upon the alloy and properties of the base strain gage material, the rolling of it into thin foil strips, and heat treatment.
Fortunately, the base material lots and the subsequent foil strip lots are very large, so that a single lot qualified at the foil strip level will constitute several years’ supply. The qualification of a foil strip lot involves performing nominal heat treating of test samples followed by testing at 0°, 75°, and 150°F. The Temperature Effect on Output is then calculated on a chord slope basis and verified to be within the 0.0008%/°F specification for the two resulting temperature intervals.
On a production basis, sub lots are formed from the strip lots and heat treated. Each sub lot is then qualified for Temperature Effect on Output by testing. These sub lots are small enough that tests are being conducted about weekly. The test consists of collecting samples of gages from a specified distribution within the sub lot and installing these gages into load cell flexures representative of the style and material for which the gages are destined. Four flexures are gages, each with 8 gages. They are then tested at temperatures of 75° and 150°F. The test criteria applied to the chord slopes over this interval is 0.0008%/°F.
The sub lots which pass the criteria are made available for production of load cells of the appropriate style and material. Lots which fail are scrapped. Due to good gage uniformity and monitoring of process trends, lot yield is relatively high.
The testing of individual production load cells for Temperature Effect on Output is prohibitively expensive. The above procedure of lot qualification produces load cells which meet specifications with a high degree of confidence at a reasonable cost.
The temperature rating of a strain gage type load cell is primarily dependent upon the materials selected for its construction. While the load bearing element is normally good for a relatively wide temperature range, the non-metallic materials in a load cell are quite sensitive to temperature extremes and must be properly selected. This includes strain gage materials, adhesives, and insulations. Most Interface load cell models are rated for an upper operating temperature limit of 200°F. Special models can be made to operate as high as 500°F.
With any set of materials, performance at temperature extremes is nearly always compromised to some extent, relative to performance at nominal temperatures. There are four parameters of interest in examining temperature performance of high temperature cells.
A) Temperature Effect on Zero
The change in zero balance that is due to a change in ambient temperature. It is normally expressed as the slope of a chord spanning the compensated temperature range.
B) Temperature Effect on Output
The change in output that is due to a change in ambient temperature. It is normally expressed as the slope of a chord spanning the compensated temperature range. Note that output is defined as a net value, as the zero load signal is always subtracted from the loaded signal.
C) Creep
The change in load cell signal that occurs with time while under load, and with all environmental conditions and other variables remaining constant. It is normally expressed in units of % of applied load over a specified time interval.
D) Zero Return
The degree to which the initial zero balance is maintained after application and release of a load, while environmental conditions and other variables remain constant.
Download or Print Temperature Compensation of High Temperature Load Cells
This document defines the terminology and performance parameters pertaining to engineering specifications of load cell products.
The objective of this terminology standard is to promote effective communication of specifications and to constitute a reference for uniformity.
The definitions herein are generally compatible with common understanding in the load cell community and are an expansion of those found in Load Cell Terminology and Test Procedure Recommendations, Third Edition, 1985, Scale Manufacturers Association, and in OIML International Recommendation R60, 1991 Edition.
This document includes modifications to the definitions in the above referenced standards to correct some of their inconsistencies and inadequacies.
The following primer is a resource to use in selecting a torque transducer for your next project or to put in a test lab. The options are plentiful, so reviewing this guide can help you make the best decision based on your specific use case and requirements.
To start, there are two basic types of torque transducers: rotary and reaction.
A reaction or static torque transducer measures torque without rotating, while a rotary torque transducer rotates as part of the system. A rotary sensor is merely a reaction sensor that is allowed to rotate.
Normally, a reaction style sensor has a cable attached to it to supply excitation voltage to the strain gage bridge and for output of the mV/V signal. The spinning of these sensors is prevented by the attached cable. To get around the issue of the attached cable, a variety of methods have been used for rotary sensors. Some of those methods include slip rings, rotary transformers, rotating electronics, rotating digital electronics and radio telemetry.
Like a load cell, a torque transducer consists of a metal spring element or flexure. Strain gages are applied to the flexure in a Wheatstone bridge configuration. Torque applied to the sensor causes bending or shear strain in the gaged area, generating an output voltage signal proportional to torque.
Slip rings are among the original methods used for power and signal transfer. The rotating sensor has a set of metal rings pressed onto its shaft. Each corner of the strain gage bridge is connected to a ring. Carbon silver brushes slide on the rings, transferring power and signal. Slip ring sensors are usually not recommended for continuous or high RPM use because of wear in the brushes, which causes dust and creates noise in the signal. Slip-ring sensors require periodic cleaning and brush replacement. An advantage of slip-ring style sensors is they can be used with traditional mV/V instrumentation.
Another commonly used method involves rotary transformers. This method uses a set of transformers, one to carry the excitation voltage onto the shaft and the other to transfer the signal off. They are called rotary transformers because one winding of each transformer rotates relative to the other winding. Advantages of this approach include low noise and no wearing parts in the electrical path. Because of the AC nature of transformers, AC carrier amplifiers are required for signal conditioning. Some rotary transformer torque transducers include built-in signal conditioning, allowing for a standard DC supply voltage and a high-level signal output.
The next type of rotary torque transducer adds electronics to the rotating shaft. Unlike rotary transformer sensors, these types have strain gage amplifiers and signal converters directly on the rotating shaft. Power is still transferred inductively, but unlike rotary transformer sensors, shaft electronics condition and rectify the supply voltage, amplify the bridge output signal and convert the signal for inductive transfer back to the stator. In a simple case, the signal is converted and transferred as a frequency and then converted from frequency to DC voltage output in the stator electronics. An advantage of this approach is lower manufacturing cost since precisely wound and aligned transformers are not required.
A more complex approach involves digitization of the torque signal on the rotor. This approach adds an A/D converter, digital signal transfer across the inductive coupling, and D/A conversion in the stator. Advantages of this approach include the ability to switch a shunt resistor directly at the strain gage bridge.
When choosing a torque transducer, one of the primary considerations is selecting the right capacity. On one hand, if you choose too large a range, the accuracy and resolution may not be enough for the application. On the other hand, if you choose too small a size, the sensor may be damaged due to overload, which is an expensive mistake.
We’d much rather have happy customers with functioning systems. In the end, the customer takes final responsibility for choosing the proper size for his application.
To select the proper size, first determine the amount of torque you want to measure. This can be easy or hard, depending on your application. An easy example would be a fastener torque application, where a certain amount of torque is to be applied to a fastener. A more difficult application might be trying to figure out how much torque is required for a new design wind turbine
If there’s a motor involved, you can usually read the rated HP and RPM off the nameplate. Once you know that, average running torque can be calculated from one of the following equations:
Torque in lb-ft = (Horsepower x 5,252) / RPM
Torque in lb-in = (Horsepower x 63,024) / RPM
Torque in Nm = (Horsepower x 7,121) / RPM
After you determine the maximum average running torque of the system, the next step is to decide how much safety-factor you need to prevent overloading the sensor. In rotary torque, there is always one side of the sensor being driven, and the other side being loaded. Some drives and loads stress the torque transducer more than others. These drive and load factors must be considered when determining the maximum peak torque in the system.
Load service factors from one to four can be assigned to different types of loads, with one being the least severe. Examples of service factor one devices are smooth running, constant rpm items such as fans and centrifugal blowers. Liquid pumps and axial compressors also fall into this category.
Going up the scale, load service factor two devices are non-reversing, non-constant load or start/stop devices. Examples include briquetting machines, cranes and hoists, conveyors, extruders and mixers.
Load service factor three devices involve high variable shock or light reversing loads. Examples include crushers, single cylinder reciprocating pumps, vehicle drivelines and hammer mills.
Load service factor four devices are the most severe and involve heavy to full torque reversals including reciprocating compressors.
Next you must consider drive service factors. Much the same as loads, different types of drives offer different levels of severity, influencing the maximum expected peak torque in an application.
Drive service factor zero devices are the easiest and include turbines or smooth running DC or 3-phase AC motors. Factor 0.5 devices include 8-cylinder gas or 10-cylinder diesel engines and single-phase AC motors. Moving up the scale, drive service factor one devices include 6-cylinder gas or 8-cylinder diesel engines, and 3-phase AC motors controlled by variable frequency drives.
Examples of drive service factor 1.5 devices include 4-cylinder gas or 6-cylinder diesel and single-phase VFD controlled AC motors. Topping out the range with drive service factors from 2 to 4 include less than 4-cylinder gas and less than 6-cylinder diesel engines. Diesel engines have high compression ratios and cause torque peak s that can be 4x or 6x the average running torque, leading to rapid use of the fatigue life and premature transducer failure.
Finally, consider startup conditions. When starting a high inertia load with an electric motor, very high peak torque can result. One thing to check is the starting torque rating of the motor if you can find it. Diesel engines can also have very high starting and stopping torques of 6x running torque.
Maximum expected peak torque can be calculated by taking the above factors into consideration. Peak torque is equal to average running torque x (load service factor + drive service factor). This is the recommended capacity of your torque transducer.
For example, consider a briquetting machine being driven by a VFD controlled 3-phase AC motor. The motor is rated for 150 hp at 1790 rpm. From the equation above, calculated average running torque in Nm is (7121 * 150) / 1790 = 597 Nm. A briquetting machine has load service factor two and the VFD controlled 3-phase AC motor has a drive service factor one. Adding these together we get combined service factor three. We then multiply 3 x 597 Nm to get 1790 Nm as the expected peak torque. In this case a torque transducer of at least 1790 Nm capacity would be selected.
Once the required capacity has been determined, it’s important to consider the accuracy and resolution of the measurement. Torque transducer accuracies are usually quoted as a percentage of capacity. A common rating is 0.1% combined error. For example, 1000Nm sensor, when used anywhere within its 1000Nm rating, will have nonlinearity and hysteresis error of no more than +/-0.1% of 1000Nm, or +/-1Nm.
When measuring an average running torque of 800Nm with this sensor, the +/-1Nm may be just fine. However, if the application has a very low ratio of average running torque to maximum peak torque, it may be necessary to use this same transducer to measure a running torque of 100Nm. In this case, +/-1Nm out of 100Nm is a 1% error.
TIP: Choosing a transducer with enough capacity to survive the application can make it difficult to achieve high accuracy. As always, compromises must be made.
Another way to allow for high overloads while still accurately measuring smaller torque values is to use a multi-range sensor.
For example, if you have a system with high load and service factors you might have a relatively low running torque but high peak values. If you want to accurately measure both the running and the peak torques then a dual-range sensor would be a good choice. Ratios of high to low capacity on dual range torque transducers are typically 5:1 or 10:1. The safe overload rating of the sensor is equal to 2x the higher range
Some newer sensors, such as the Interface model AxialTQ.
Another factor to consider is resolution of the measurement signal. Analog sensors such as slip- ring or rotary transformer types have essentially infinite resolution, limited by the signal to noise ratio of the system.
Digital rotary torque transducers are subject to the bit resolution of their analog to digital converters. Typical digital sensors are 12 or 16-bit or higher. A 12-bit sensor has 4096 counts over its -Full Scale to +Full Scale range. What this means is the resolution over one direction of the measuring range (CW or CCW), is 2048 counts. For a 1000Nm 12-bit sensor, resolution is therefore about 0.5Nm. If that’s not sufficient, a higher resolution sensor should be selected. In contrast, a 16-bit 1000Nm sensor will have 0.03Nm and an 18-bit 1000Nm sensor has 0.008Nm resolution.
Torque transducers typically come in one of two major mechanical configurations, shaft or flange style. Shafts can be either smooth or keyed with keyed shafts coming in either single or double-keyed versions. Flange style sensors are typically shorter than shaft style, and have pilots on their flange faces as a centering feature.
Smooth shafts offer some advantages over their keyed counterparts, including more uniform introduction of the torque into the measuring shaft, ease of assembly and disassembly and zero backlash. A coupling designed for use with smooth shafts will have some method of clam ping to the shaft. This is commonly accomplished with split collars or shrink-disk style hubs. Shrink-disk style hubs usually include features to aid in their removal from the shaft.
Hubs for keyed shafts are simpler than those for smooth shafts and cost less but can suffer from wear due to backlash, especially in reciprocating applications. To prevent backlash, the hub must be installed on the keyed shaft with an interference fit, which is usually accomplished by either heating the hub before installation or pressing the hub onto the shaft.
Pressing of the hub risks damaging the sensor and both installation methods present problems with removal. Another less common method of installation and removal uses special hydraulic equipment. In the higher torque capacities double keyways are often used, spaced at 180 degrees around the shaft.
The two main categories of coupling are single and double flex, also referred to as half and full couplings. A single-flex coupling has flex point and allows only angular misalignment. Radial misalignment, perpendicular to the axis of rotation, is not possible. A double flex has two flex points and allows both angular and radial misalignment.
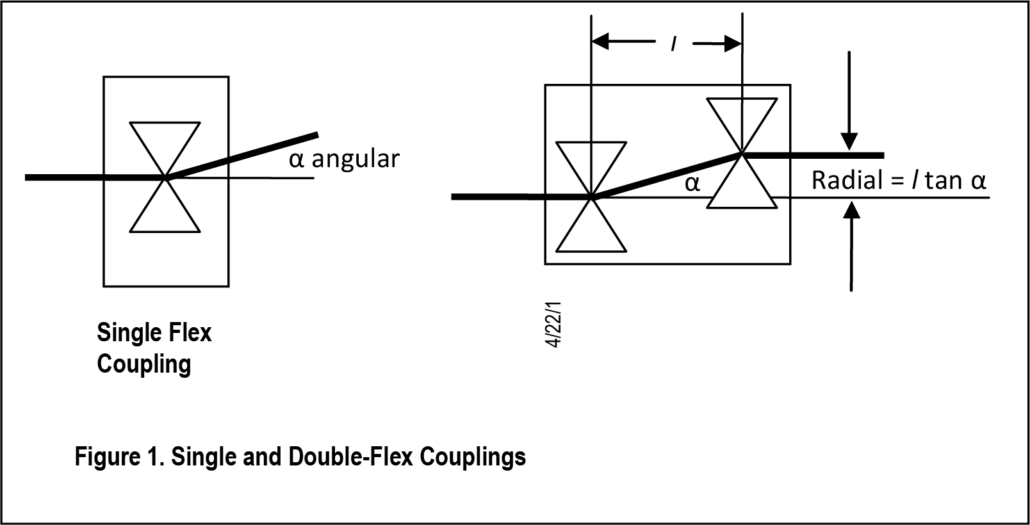
Some available styles of coupling are flexible disk couplings which are desirable for torque measurement because of their high torsional rigidity and zero backlash.
Torsional rigidity allows for fast dynamic response and low wind-up. A less rigid coupling will mechanically dampen the signal, possibly reducing or eliminating the ability to measure transient events. Another desirable quality of flexible disk couplings is they can be balanced for high RPM operation.
Rotary torque transducers come either supported on bearing in a housing or are bearingless. Bearing supported designs maintain alignment between the rotating and stationary parts of the sensor and can be easier to mount. Bearingless sensors require the non-rotating part of the sensor to be held in a precisely fixed position relative to the rotating part. Some bearingless sensors are more forgiving of alignment issues than others.
There are two main methods of mounting rotary torque transducers, fixed or floating. Fixed mount applies only to sensors with bearings and involves attaching the sensor housing to a fixed support.
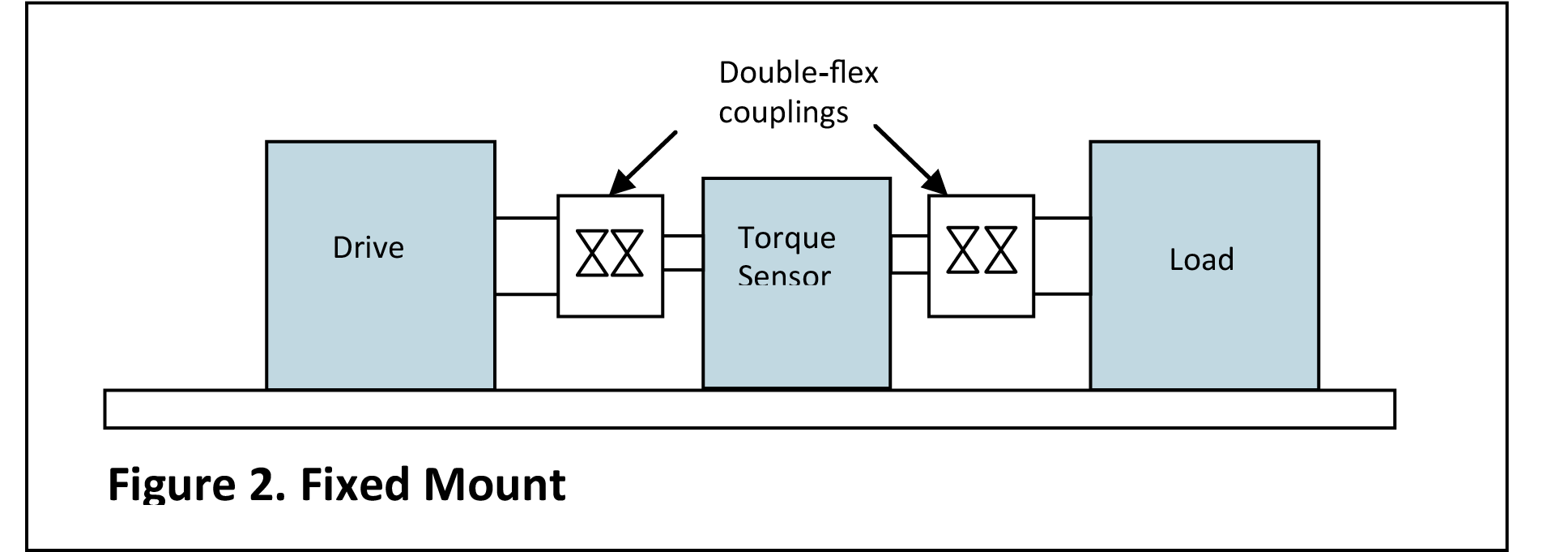
In floating installations, the sensor is supported only by its drive and load side connections, which are typically single-flex style couplings. A flexible strap keeps the torque transducer housing from rotating. Bearingless sensors are always floating mount.
Fixed mounting requires that the sensor housing have a means to attach it to the support. Sometimes the mount is an option on the sensor and sometimes the foot or pedestal mount is built as part of the sensor. The simplest fixed-mount design sensors include a flat machined surface on the housing with threaded mounting holes. In fixed mount installations, double flex couplings must be used.
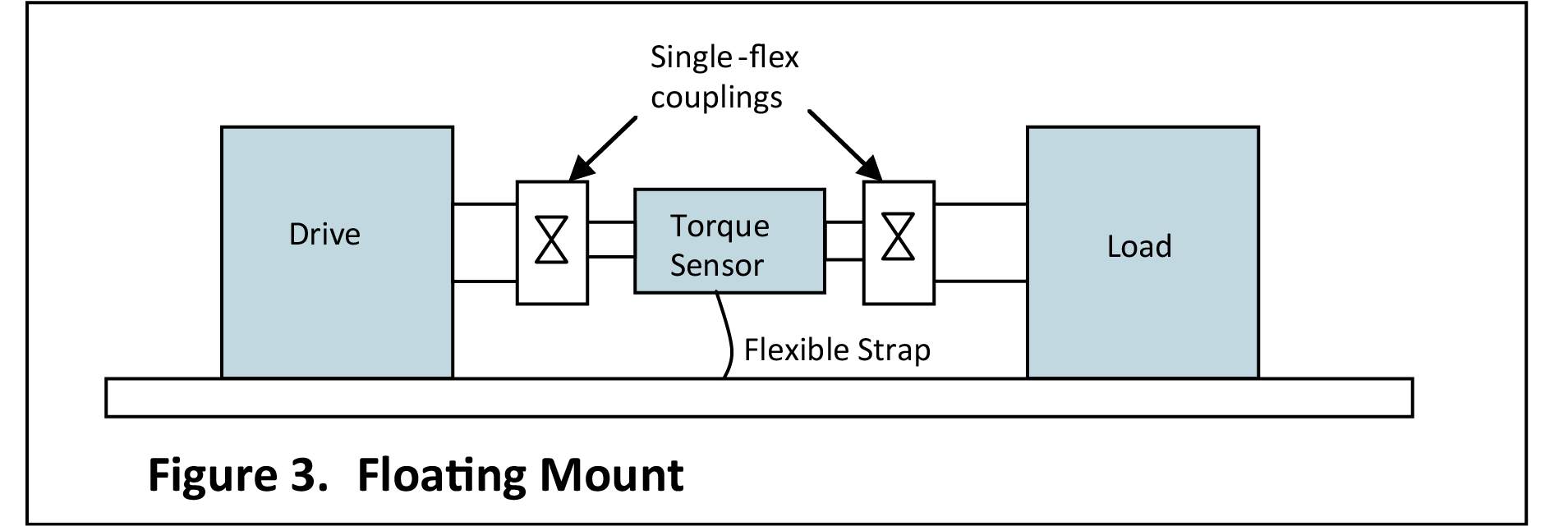
Fixed mount can be better for high rpm use, limiting the lengths of the unsupported rotating sect ions. Foot or pedestal mounted sensors are not designed to be used as bearing blocks, so ca re must be taken to ensure against unduly loading the bearings. An example of a fixed mount application is electric motor testing, where it’s important to quickly move motors in and out of the test stand. By mounting the torque transducer and load to a fixed plate, the alignment between the two can be set once and maintained indefinitely. The test motor can then be coupled and uncoupled from the sensor with no worries about the sensor losing its support each time the motor is disconnected. In contrast, if the sensor is float mounted, each time t he motor is disconnected the torque transducer must be supported from drooping.
Floating mounts are more forgiving of misalignment between the drive and load. A floating sensor, mounted between two single-flex couplings, is essentially a long double-flex coupling. Since the allowable radial misalignment is directly proportional to the distance between flex points, the floating mount installation is more tolerant of misalignment between the drive and load.
Another advantage of floating mounts is the reduction of the effect of extraneous loads on the sensor. For example, in a floating mount system, a thrust load is carried only by the sensing element with no effect on the bearings. In a fixed mount installation, any thrust load becomes a load on the bearings, causing premature wear in the bearing and possibly contact between the rotating and stationary parts if the shaft shifts within the housing. The thrust load rating of a floating mount sensor is typically orders of magnitude greater than a fixed mount.
As with any sensor, environmental factors must be considered. Some things to consider are temperature and exposure to moisture or dust. For temperature, rotating torque transducers usu ally have a storage range, an operating range and a rated or compensated range.
The storage range is the temperature over which the sensor can be stored without damage. While it won’t hurt the sensor to store it within this range, it must be used within its operating range, or it might be damaged. The compensated or rated range is the temperature over which the torque transducer is guaranteed to meet its published temperature specifications. Depending on the sensor, the temperature performance will be two or more times worse when outside the rated range. If the sensor must be exposed to temperature extremes, then steps should be taken to shield or protect it. Heating blankets or enclosures are sometimes used.
Another environmental factor to consider is electrical noise. Some installations are noisier than others, especially where electric motors and/or variable- frequency drives are employed. Variable-frequency drives (VFD) are used to control the speed of an AC electric motor by controlling the frequency of the electrical power supplied to the motor. Other names for VFD are adjustable-speed drives (AFD), AC drives, inverter drives or variable-speed drives (VSD).
When a torque transducer is used in conjunction with a VFD, proper grounding and shielding techniques must be used to prevent torque transducer malfunction. During operation, a VFD creates noise on the power line and radiates noise from the VFD-to-motor cable. Noise is also capacitively coupled from the motor windings into the motor shaft and through the bearings into the motor frame, and from unshielded motor leads in a conduit to the conduit supports.
To ensure a successful installation, the VFD supplier grounding recommendations should be followed, including use of a shielded motor feed cable.
In rotating torque measurement, the sensor will be spinning, so it’s important to know what the maximum RPM will be and to make sure the torque transducer can withstand it. Limiting factors may be bearing life, rotating electronics or balancing, depending on the type of sensor. You must also consider the limits of other parts in the rotating assembly such as couplings. Typically, rotating parts will have a published rpm limit. Sometimes those limits can be increased with special balancing or special component parts. If in doubt, please check with the sensor provider.
Rotating torque measurement is rarely a steady value, more commonly varying around some average value. In certain only the average torque is important, but in other cases the transient torque peaks are of interest. In either case it’s important to understand the sampling rate and/or measurement bandwidth of the system.
Rotating torque transducers should always list a measurement bandwidth and/or a sampling rate on their data sheets. Depending on the type, bandwidth can range from a couple of hundred Hz to several thousand or more. An application where average running torque is typically measured is engine dynamometers. In this case you may not care about torque spikes caused by individually firing cylinders so they can be filtered out, either by the sensor or in the data acquisition electronics.
In other cases, the peaks and valleys of the torque signal are important, and a sensor with enough bandwidth must be selected. For example, in an end of assembly line gearbox test it may be important to check if one of the individual gear teeth is broken or if the gears aren’t seated properly. This could be determined by comparing the torque signature of the tested part to a known good one. In a 1:1 ratio right-angle gearbox with 60-tooth gears spinning at 500 rpm, a tooth engages 500 times per second.
To accurately profile the tooth engagement, you would need a torque transducer with bandwidth of at least 500 Hz.
The proper selection of a torque transducer can be confusing when considering the variables, specifications and use cases. Careful attention must be given to proper capacity, speed, connection, mounting and environment. Interface Application Engineers are an excellent resource to assist you in defining your requirements. You can also find a useful tool online, the Interface Torque Selection Guide, to get you started in your review.
Performance of a load cell force (or weigh) measurement system is dependent upon the integrity of the physical installation, correct interconnection of the components, proper performance of the basic components which make up the system, and calibration of the system. Presuming that the installation was originally operating and was calibrated, troubleshooting can begin by checking the components individually to determine if they have been damaged or have failed.
The basic components are:
Load Cells which are not mounted in accordance with the manufacturer’s recommendations may not perform to manufacturer’s specifications. It is always worthwhile to check:
Proper hardware (thread sizes, jam nuts, swivels, etc) as required to connect the load to the load cell. A fundamental requirement is that there be one, and only one load path! This load path must be through the load axis of the load cell. This may sound elementary, however it is a commonly overlooked problem.
Proper load cell performance is also dependent upon the electrical “system.” The following items are common problem areas:
Loading of the bridge circuit. (Highly accurate load cell systems require highly accurate read-out instruments. Such instruments typically have very high input impedances to avoid circuit loading errors.)
It is quite easy to make a quick diagnostic check of a load cell. The procedure is quite simple and a minimum of equipment is required. Should it be determined that the load cell is at fault, the unit should be returned to the factory for further evaluation and repair as may be required. Many of the checks may be performed with an ohmmeter.
(Numbers apply to standard 350 ohm bridges.)
If the ohmmeter resolution is 0.1 ohm or better, then a computed Zero Offset of greater than 20 percent is a clear indication of overload. A computed zero balance of 10-20% is an indication of probable overload. If the load cell has been overloaded, mechanical damage has been done that is not repairable, because overloading results in permanent deformation within the flexural element and gages, destroying the carefully balanced processing that results in performance to Interface specifications. While it is possible to electrically re-zero a load cell following overload, it is not recommended because this does nothing to restore the affected performance parameters or the degradation to structural integrity.
If the degree of overload is not severe the cell may in some cases be used at the user’s discretion, although some performance parameters may violate specifications and the cyclic life of the load cell may be reduced.
The tests described above can be performed using a standard ohm meter, although best results are obtained with a megohm meter. If resistance
is beyond the standard ohmmeter range, about 10 megohms, the cell is probably OK. However, some kinds of electrical shorts show up only when using a megohm meter or with voltages higher than most ohmmeters can supply.
If the load cell is defective for reasons other than overload, return to factory for detailed evaluation. Factory evaluation may show that the cell is repairable or non-repairable and if repair or replacement will be under warranty. If non-warranty, the customer will be contacted with the cost of repairs and recalibration, and a delivery date after receipt of authorization to proceed.
Dependent on option code. Standard internally amplified load cells such as a low profile load cell receive a standard calibration with applied load vs. voltage calibration points. ISO/IEC 17025:2017 accredited calibrations are available for voltage outputs. Current (mA) outputs are not within our ISO/IEC 17025:2017 accredited scope.
A load cell/amplifier system level calibration can be accomplished in one of two ways:
A load cell and indicator system level calibration can be accomplished in one of two ways:
Standard load cells with TEDS chips installed have the standard mV/V calibration certificate for its respective model as well as a TEDS data sheet to report what data is stored on the TEDS chip per IEEE 1451.4, template 33. To provide system level traceability, any indicator to be paired with a TEDS load cell should have a traceable internal mV/V calibration performed. ISO/IEC 17025:2017 accredited calibrations are available for the both the internal mV/V indicator calibration and the load cell calibration. An in-rig system calibration using applied loads can also be performed to verify and record system performance.
Dependent on option code. Standard internally amplified load cells such as a low profile load cell receive a standard calibration with applied load vs. voltage calibration points. If the amplifier span or zero does not require adjustment, a combined “As-Found and Final” calibration certificate is provided. If the amplifier is adjusted, separate “As-Found” and “Final” certificates are provided. The “As-Found” certificate reports the calibration results before adjustment, the “Final” certificate reports the condition after final adjustment. ISO/IEC 17025:2017 accredited calibrations are available for voltage outputs. Current (mA) outputs are not within our ISO17025 accredited scope.
A load cell/amplifier system level recalibration is most commonly performed using method (A) described below. Method (B) can also be used, but would not document the as-found condition of the system.
A load cell/Indicator system level recalibration is most commonly performed using method (A) described below. Method (B) can also be used, but the as-found condition of the system would not be documented. Load cells used with the Interface Gold Standard System or with the Interface 9840 are addressed in method (C).
Standard load cells with TEDS chips installed have the standard mV/V “As-Found and Final” calibration certificate for its respective model as well as a TEDS data sheet to report what data was stored on the TEDS chip per IEEE 1451.4, template 33. To provide system level traceability, any indicator to be paired with a TEDS load cell(s) should have a NIST traceable internal mV/V calibration performed. ISO/IEC 17025:2017 accredited calibrations are available for the internal mV/V Interface indicator calibrations.
System level recalibration of TEDS enabled load cell with a compatible indicator has the below steps performed:
Where applicable, shunt calibration readings or outputs are recorded as part of the load cell or load cell and amplifier system calibration. The shunt calibration data provides a means for the user in the field to verify system scaling, and as many instruments can be scaled using this data it provides a means to temporarily restore a calibration in the field.
| Shunt (+/- 0.01%) |
Output | Straight Line Conversion |
Connections* | |
| Tension Compression |
60.0 KOhm 60.0 KOhm |
1.45393 mV/V – 1.45464 mV/V |
1817.7 N 1818.1 N |
– Out to – Exc – Out to + Exc |
*For models wired with + Sense, – Sense or – SCal leads, resistor connections are actually to these leads in place of + Exc, – Exc, or – Out respectively. |
||||
Performance of a load cell force (or weigh) measurement system is dependent upon the integrity of the physical installation, correct interconnection of the components, proper performance of the basic components which make up the system, and calibration of the system. Load Cell Troubleshooting begins with checking if the installation was originally operating and was calibrated, load cell troubleshooting can begin by checking the components individually to determine if they have been damaged or have failed.
The basic components are:
Load Cells which are not mounted in accordance with the manufacturer’s recommendations may not perform to manufacturer’s specifications. It is always worthwhile to check:
Proper hardware (thread sizes, jam nuts, swivels, etc) as required to connect the load to the load cell. A fundamental requirement is that there be one, and only one load path! This load path must be through the load axis of the load cell. This may sound elementary, however it is a commonly overlooked problem.
Proper load cell performance is also dependent upon the electrical “system.” The following items are common problem areas:
It is quite easy to make a quick diagnostic check of a load cell. The procedure is quite simple and a minimum of equipment is required. Should it be determined that the load cell is at fault, the unit should be returned to the factory for further evaluation and repair as may be required. Many of the checks may be performed with an ohmmeter.
(Numbers apply to standard 350 ohm bridges.)
If the ohmmeter resolution is 0.1 ohm or better, then a computed Zero Offset of greater than 20 percent is a clear indication of overload. A computed zero balance of 10-20% is an indication of probable overload. If the load cell has been overloaded, mechanical damage has been done that is not repairable, because overloading results in permanent deformation within the flexural element and gages, destroying the carefully balanced processing that results in performance to Interface specifications. While it is possible to electrically re-zero a load cell following overload, it is not recommended because this does nothing to restore the affected performance parameters or the degradation to structural integrity.
If the degree of overload is not severe the cell may in some cases be used at the user’s discretion, although some performance parameters may violate specifications and the cyclic life of the load cell may be reduced.
The tests described above can be performed using a standard ohm meter, although best results are obtained with a megohm meter. If resistance is beyond the standard ohmmeter range, about 10 megohms, the cell is probably OK. However, some kinds of electrical shorts show up only when using a megohm meter or with voltages higher than most ohmmeters can supply.
Never use a voltage higher than 50 VDC or 35 VRMS AC to measure insulation resistance, or breakdown of the insulation between the gages and the flexure may result. Low resistance (below 5000 megohms) is often caused by moisture or pinched wires. The cause and extent of damage must be established at the factory to determine if the load cell may be salvaged.
If the load cell is defective for reasons other than overload, return to factory for detailed evaluation. Factory evaluation may show that the cell is repairable or non-repairable and if repair or replacement will be under warranty. If non-warranty, the customer will be contacted with the cost of repairs and recalibration, and a delivery date after receipt of authorization to proceed.
We use cookies to enhance your browsing experience, serve personalized content, and analyze our traffic. By clicking "Accept All Cookies", you consent to our use of cookies.
Accept All CookiesReject AllCookie SettingsWe may request cookies to be set on your device. We use cookies to let us know when you visit our websites, how you interact with us, to enrich your user experience, and to customize your relationship with our website.
Click on the different category headings to find out more. You can also change some of your preferences. Note that blocking some types of cookies may impact your experience on our websites and the services we are able to offer.
These cookies are strictly necessary to provide you with services available through our website and to use some of its features.
Because these cookies are strictly necessary to deliver the website, you cannot refuse them without impacting how our site functions. You can block or delete them by changing your browser settings and force blocking all cookies on this website.
These cookies collect information that is used either in aggregate form to help us understand how our website is being used or how effective our marketing campaigns are, or to help us customize our website and application for you in order to enhance your experience.
If you do not want us to track your visit to our site, you can disable tracking in your browser here:
We also use different external services like Google Webfonts, Google Maps and external Video providers. Since these providers may collect personal data like your IP address we allow you to block them here. Please be aware that this might heavily reduce the functionality and appearance of our site. Changes will take effect once you reload the page.
Google Webfont Settings:
Google Map Settings:
I agree to the terms and conditions laid out in the Privacy Policy



Please share your location to continue.
Check our help guide for more info.